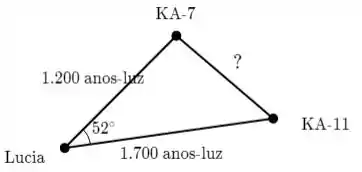
Ainda faltam dois sistemas solares para Lúcia visitar em sua viagem, mas sua espaçonave está com pouco combustível. O primeiro sistema, KA-7, está a 1.200 anos-luz (a.l.) de distância, enquanto o segundo sistema, KA-11, está a 1.700 a.l. Sua prioridade é visitar o sistema solar KA-7. Para determinar se ela também poderá visitar o KA-11, é preciso calcular a distância entre KA-7 e KA-11. Se Lúcia vê um ângulo de 52o entre KA-7 e KA-11, qual é a distância entre KA-7 e KA-11?
Passo 1
Fala aí, maninho! Apesar de toda estória que veio escrita no enunciado, tudo que a gente precisa fazer é calcular o lado que falta do triângulo da ilustração. Pra isso, a gente vai precisar de trigonometria.

Cara, infelizmente, o enunciado não disse em lugar nenhum que esse triângulo é retângulo, e na ilustração também não tem o quadradinho que indica isso. Isso complica um pouco as coisas.

Mas calma, a gente pode resolver usando a lei dos cossenos! Você lembra dela? GOOGLE:
![]()
É basicamente o teorema de pitágoras aplicado em um triângulo qualquer (sem necessariamente ser triângulo retângulo).

Sendo teta o ângulo entre a e b, e c sendo o lado que a gente desconhece do triângulo, então a nossa equação fica assim:
![]()
Prontinho! Agora a gente só precisa resolver essa conta e vamos ter, de cara, o tamanho do cateto que o enunciado tá pedindo.

Mas, como o exercício é de Prog, vamos esquecer a calculadora e fazer essa conta usando Python, ok?!
Passo 2
Pô, a gente vai ter que usar raiz quadrada e função cosseno pra resolver aquela equação que a gente chegou. E essas funções não vem por padrão, a gente precisa importar elas do módulo math. Pra isso, a gente usa a palavra-chave “import” seguido do módulo que a gente quer importar.
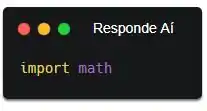
Pronto! Agora temos acesso às funções matemáticas de Python, e já pode fazer as nossas contas usando essas funções!

Mas antes, vamos passar as variáveis do problema pra Python também.
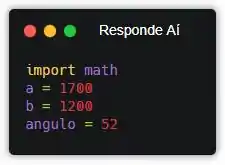
Prontinho! O enunciado deu o ângulo em graus, e a gente escreveu ele ali. Mas lembra que as funções do módulo math sempre consideram que a gente tá usando radianos?! Então, precisamos converter esses 52 graus pra radianos antes de usar...

A gente pode converter direto na hora de criar a variável usando a função math.radians(). Se liga em como fica:
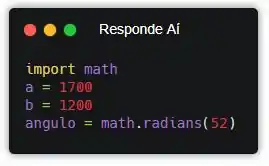
Agora sim! O ângulo tá salvo na variável, mas em radianos. Só falta a gente fazer a conta!
Passo 3
Bora traduzir nossa equação pra Python! Fica mais ou menos assim:
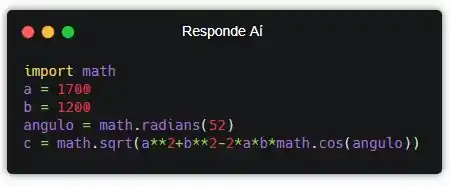
Grande pra caraca! Mas é isso mesmo… Agora, já vamos ter o tamanho do lado que falta no triângulo do enunciado. Mas a gente ainda precisa descobrir qual é!

Então, vamos exibir o resultado da conta usando a função print()!
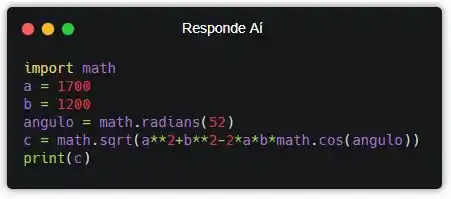
Agora sim! Ao executar esse programa, ele exibirá o tamanho que foi calculado na variável c:
![]()
Ok, essa é a resposta. Mas não tá legal não! Vamos usar formatação de string pra arredondar pra duas casas decimais.
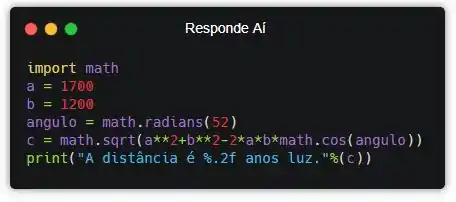
Beleza! Vamos executar de novo e ver como vai ficar o resultado.
![]()
Bem melhor, né?! E essa é a resposta da nossa questão! Finalizamos!

Te vejo no próximo, doido! Valeuuuuu
Resposta
![]()