Possuo 4 bolas amarelas, 3 bolas vermelhas, 2 bolas azuis e 1 bola verde. Pretendo colocá-las em um tubo acrílico translúcido e incolor, onde elas ficarão umas sobre as outras na vertical. De quantas maneiras distintas podemos formar essa coluna de bolas?
Passo 1
E aí, maninho! Se liga nesse exercício de combinação que caiu na PUC. Eu MORRIA de medo de análise combinatório no ensino médio.

Agora eu continuo morrendo de medo, mas pelo menos é na faculdade!

A ideia do enunciado é que as bolinhas vão sem empilhadas, e o professor quer que a gente descubra quantas formas diferentes de arrumar essas bolinhas existem. Bom, vamos pensar num problema um pouquinho menor aqui só pra gente pegar a ideia...
Passo 2
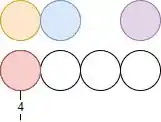
Se liga, imagina que a gente tem 4 bolinhas e 4 buraquinhos pra encaixar as bolinhas.

Cara, a ideia é que, no primeiro buraco a gente tem todas as bolinhas na mão ainda… A gente pode colocar qualquer uma das 4, certo? Temos 4 opções. Vamos escolher uma aleatoriamente aqui no nosso exemplo, e vou escrever embaixo quantas opções a gente tinha pra escolher na hora.
Pronto! Agora, no buraquinho seguinte, a gente pode colocar qualquer uma das outras que sobraram. E sobraram 3! Então a gente tem 3 opções de bolinhas pra colocar no segundo buraquinho ali. Vou escolher a azul agora.
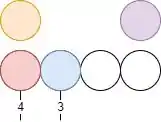
A gente tinha 3 opções na hora de escolher, e escolhemos a azul… Vamos repetir o processo mais duas vezes!
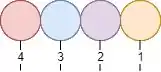
Pronto! A gente organizou as bolinhas de uma forma qualquer, aleatória que eu mesmo escolhi na hora de fazer a ilustração. Mas o importante é pensar em quantas opções a gente tinha na hora de escolher a bolinha. Se a gente multiplicar as opções que a gente tinha em cada etapa, a gente vai ter a quantidade de possíveis combinações! Nesse caso:
![]()
Talvez tu não tenha reconhecido, mas isso é a mesma coisa que 4 fatorial.
![]()
Generalizando: a quantidade de combinações possíveis é a quantidade de bolinhas fatorial. Mas quando temos duas ou mais bolinhas iguais, caímos eu outro problema.
Passo 3
Adicionei mais uma bolinha e coloquei na frente das outras. Se liga em como ficou o nosso mesmo exemplo agora:
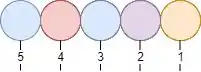
Show! Parece que a gente tem 5 fatorial de possíveis combinações agora. Mas cara, o que acontece se a gente trocar a primeira bolinha com a terceira??

Olha:
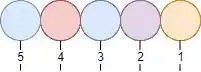
Isso aí mesmo que você tá pensando! Não mudou nada, doido! Como as bolinhas são iguais, não faz diferença se a gente trocar elas de lugar. Então, na verdade, essa combinação é igual a anterior. Por isso, a gente não precisa contar com ela. Pra gente descartar bolinhas iguais, a gente só precisa dividir o total de combinações pela quantidade fatorial de cada bolinha. Nesse caso:
![]()
Show! Sacamos a ideia… Generalizando as combinações com elementos iguais, a gente chega nessa fórmula:
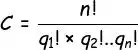
Onde n é a quantidade total de bolinhas e q é a quantidade de cada tipo de bolinha. Partiu escrever essa lógica em Python!

Passo 4
Primeiramente, vamos começar importando o módulo math. Assim, a gente vai ter acesso as funções matemáticas que vêm no Python. Dentre elas, a função math.factorial().
Pronto! Lembra de colocar o import sempre no início do programa, jae?!

Agora, vamos criar uma variável e calcular o total de combinações. Vou chamar a variável de C só pra economizar espaço. Lembrando que o total de bolinhas e a quantidade de cada uma são dados do enunciado...
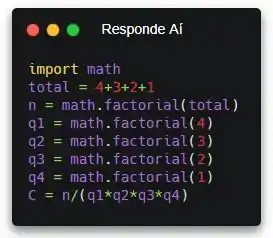
Pronto! Agora a gente só precisa exibir a quantidade de combinações.

Passo 5
Pra exibir a resposta, a gente vai usar a função print(). A danadinha tá em todas.

Mas a gente também vai usar formatação de string, que seria legal você estar sabendo! Caso não saiba do que eu tô falando, dá uma lida rápida no tópico Operações com String. É rapidinho, juro!
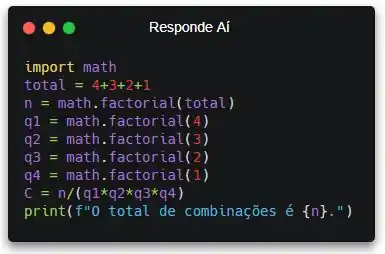
Aí sim! Agora, quando a gente executar, o número de combinações vai ser calculado e exibido pra gente.
![]()
E parece que são MUITAS combinações! hahahah

Chegamos ao nosso resultado e finalizamos a questão. Te vejo no próximo exercício, maninho!
Resposta
O total de combinações é 12600.