Determine e resolva equação da estrutura dada abaixo. Dado:
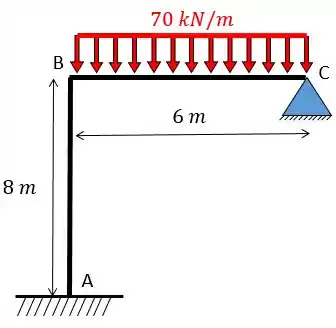
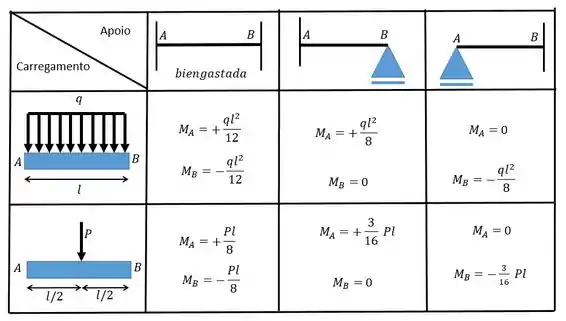
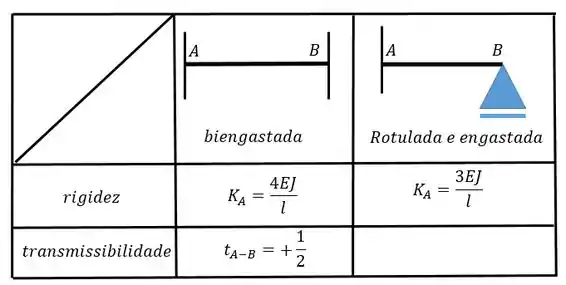
Utilize as seguintes tabelas:
Passo 1
Fala, pessoal!!! A questão pede para determinarmos as equações que regem esse problema e para isso a primeira coisa que devemos fazer é saber trocar corretamente os apoios. Neste caso só vamos precisar impedir a rotação em obtendo:
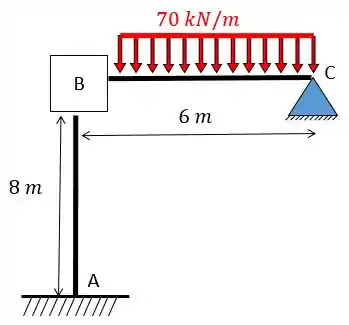
Agora sabemos que temos 1 chapas na nossa estrutura, como podemos ver ali em cima. Como temos apenas uma chapa vamos ter uma equação da forma:
Mas a questão não para aí né, a gente tem que achar os valores de e também! Vamos ver isso com mais detalhes nos próximos passos!
Passo 2
Para determinar os valores desses coeficientes nós precisamos combinar o carregamento com a condição dos apoios através da tabelinha:
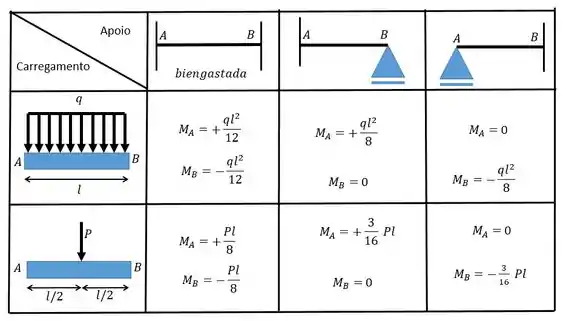
Vamos descobrir primeiro o valor de então!
Olhando a conta para cara barra teremos que:
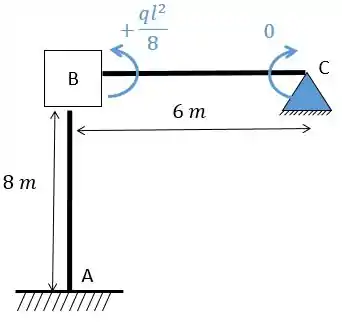
Perceba que não há carga na barra !
Substituindo os valores vamos ter:
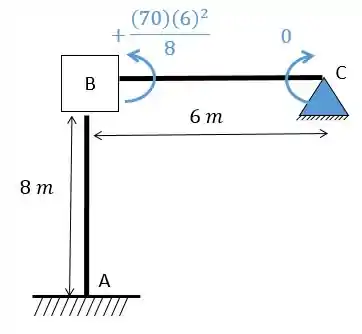
Ou seja, o valor de é:
Passo 3
Agora vamos calcular . Para isso vamos precisar da outra tabelinha:
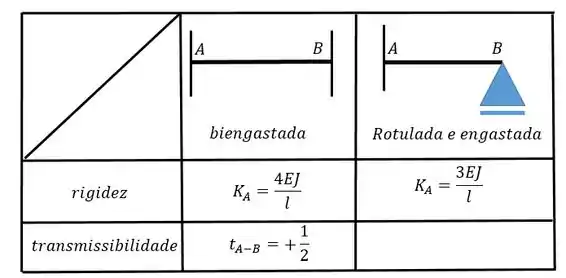
Vamos rotacionar a chapa e obtemos:
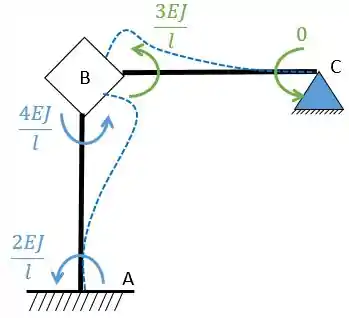
Dessa forma vamos ter:
Passo 4
Organizando o sistema temos que:
Substituindo:
E podemos calcular a deformação: