Determine as seguintes rigidezes: (
Passo 1
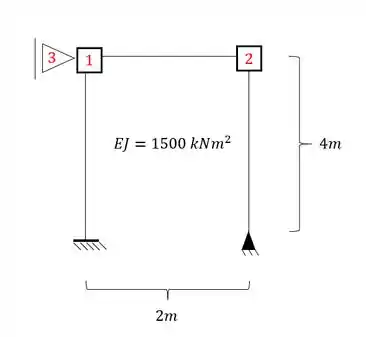
Sabemos que temos 2 chapas na nossa estrutura e um apoio do primeiro gênero, como podemos ver ali em cima. Uma parada legal a ser feita é contabilizar tudo que devemos determinar em cada chapa e apoio , se fizermos isso obtemos o seguinte:

Como não temos carregamento, não precisamos determinar , nem e nem .
Passo 2
Agora vamos rotacionar a chapa 1, para podermos determinar os valores de , e .
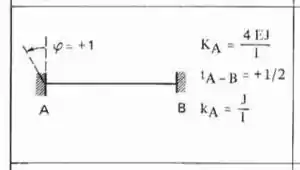
Perceba que as duas barras que chegam na chapa 1 são Bi-engastadas, logo a fórmula a ser usada é:
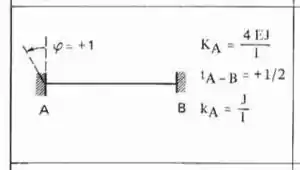
Substituindo certinho temos que:
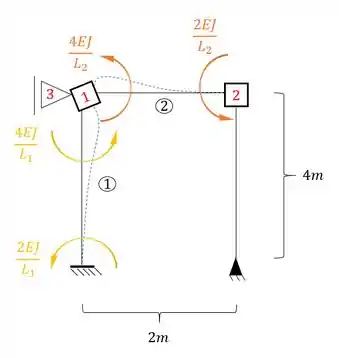
Juntando o que têm-se em cada nó, teremos que:
Para o valor de precisamos fazer a reação de apoio, sendo assim teremos que:
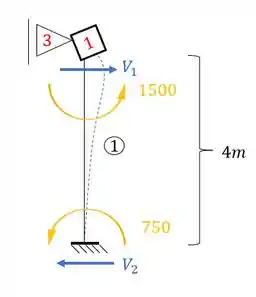
O que podemos admitir para facilitar o cálculo é que o sentido da reação do apoio do primeiro gênero é no mesmo sentido da reação que calculamos na barra, ou seja, se acharmos V1 pra frente, o final é positivo porque a reação no apoio é positiva. Logo:
Obs:. Isso acontece porque a reação que calculamos age na estrutura, ou seja, temos que passar ela com o sinal invertido para saber como ela age no apoio ( ou seja, ela está para frente da maneira que calculamos, mas invertemos o seu sentido para ela agir no apoio, ou seja, para trás. Se ele age para trás no apoio, qual vai ser a reação do apoio? Pra frente, certo? Ou seja, o mesmo sentido do vetor que calculamos ali em cima, que é pra frente, viu como assim é mais complexo? Então só lembrar que a reação de apoio tem o mesmo sentido do vetor calculado, que fica tudo lindo.
Passo 3
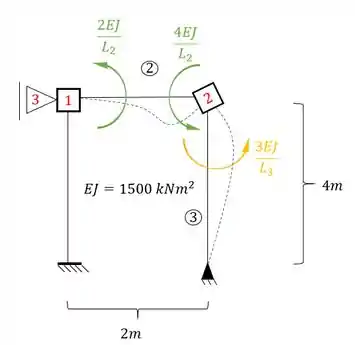
Agora vamos rotacionar a chapa 2, para podermos determinar os valores de , e .
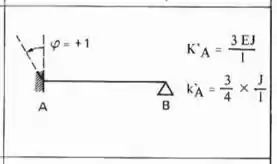
Perceba que a barra horizontal que chega na chapa 2 é Bi-engastadas, e a barra vertical que chega na chapa 2 é engastada e apoiada, logo as fórmulas a serem usadas são:
Substituindo certinho temos que:
Juntando o que têm-se em cada nó, teremos que:
Perceba que a única barra a dar reação horizontal é a barra 3, sendo assim teremos que:
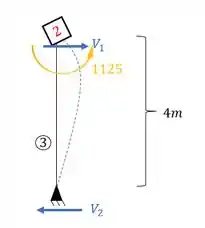
O que podemos admitir para facilitar o cálculo é que o sentido da reação do apoio do primeiro gênero é no mesmo sentido da reação que calculamos na barra, ou seja, se acharmos V1 pra frente, o final é positivo pra frente porque a reação no apoio é positiva pra frente. Logo:
Passo 4
Agora perceba que temos o apoio 3, certo? Nesse caso não rotacionamos, mas deslocamos o nosso apoio de 1 unidade, para podermos determinar os valores de , e .
Quando movimentarmos o apoio, ele afetará TODAS as barras verticais, por isso temos que tomar cuidado, e como se trata de deslocamento e não de rotação, a nossa fórmula será.
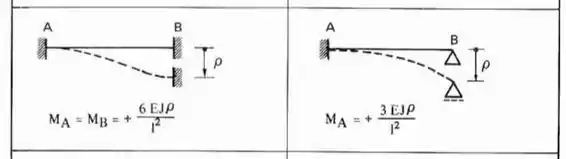
Perceba que a barra vertical da esquerda é Bi-engastada, logo usaremos uma das fórmulas, e para outra que é engasta e apoiada usaremos a outra, sendo assim teremos que:
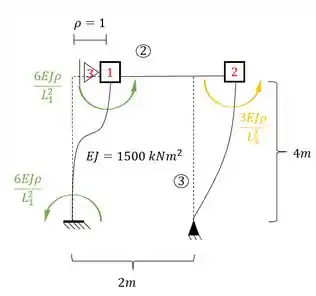
Juntando o que têm-se em cada nó, teremos que:
Perceba que as duas barras produzem reações horizontais que serão armazenadas no nosso apoio do primeiro gênero. Sendo assim teremos que:
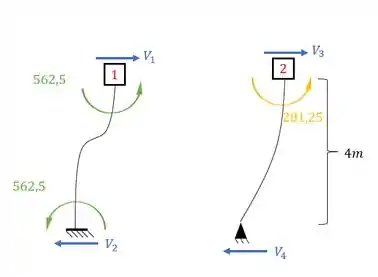
Como V1 e V3 são iguais aos valores das suas respectivas barras, e são as reações na mesma altura no apoio do primeiro gênero, basta somarmos a fazermos o macete de mantermos o sentido da reação calculada, que obtemos que o nosso será dado por:
E assim determinamos todas as rigidezes pedidas.