Determine o sistema de equações da estrutura dada abaixo:
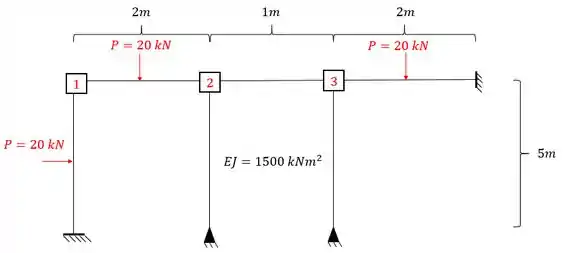
Passo 1
Sabemos que temos 3 chapas na nossa estrutura, como podemos ver ali em cima. Uma parada legal a ser feita é contabilizar tudo que devemos determinar em cada chapa, se fizermos isso obtemos o seguinte:

Sabendo já o que tem que determinar, vamos fazer um de cada vez.
Passo 2
Vamos determinar primeiro os valores de , e . Para determinar isso precisamos da seguinte tabela:
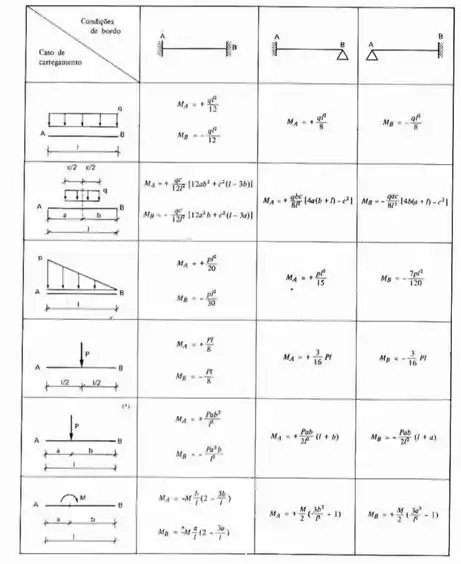
Olhando a conta para cara barra teremos que:
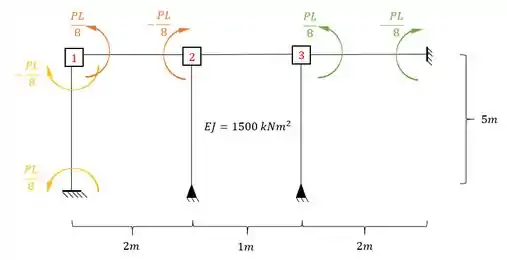
Trocando os valores teremos que:
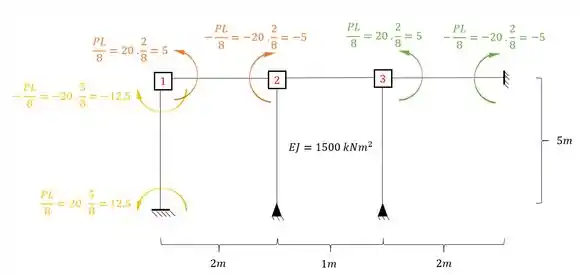
Assim teremos que:
Passo 3
Agora vamos rotacionar a chapa 1, para podermos determinar os valores de , e .
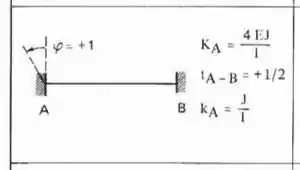
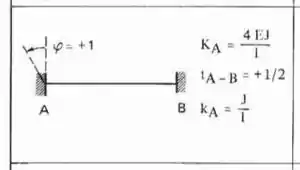
Perceba que as duas barras que chegam na chapa 1 são Bi-engastadas, logo a fórmula a ser usada é:
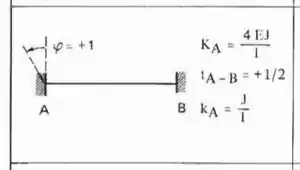
Substituindo certinho temos que:
Juntando o que têm-se em cada nó, teremos que:
Passo 4
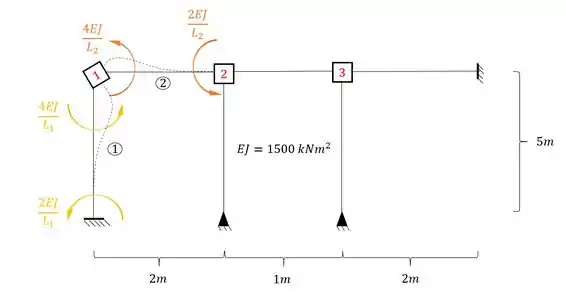
Agora vamos rotacionar a chapa 2, para podermos determinar os valores de , e .
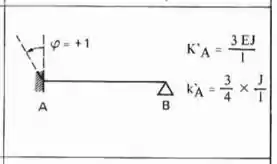
Perceba que as duas barras horizontais que chegam na chapa 2 são Bi-engastadas, e a barra vertical que chega na chapa 2 é engastada e apoiada, logo as fórmulas a serem usadas são:
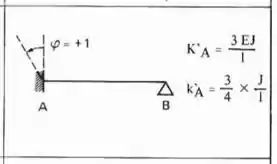
Substituindo certinho temos que:
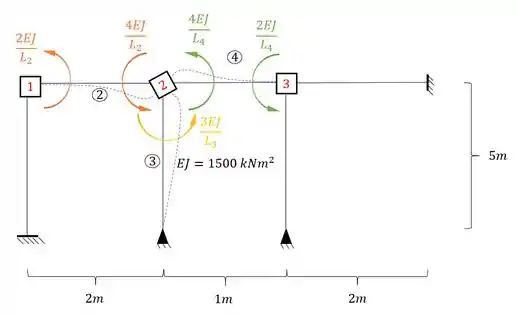
Juntando o que têm-se em cada nó, teremos que:
Passo 5
Agora vamos rotacionar a chapa 3, para podermos determinar os valores de , e .
Perceba que a barra horizontal que chega na chapa 3 é Bi-engastadas, e a barra vertical que chega na chapa 3 é engastada e apoiada, logo as fórmulas a serem usadas são:
Substituindo certinho temos que:
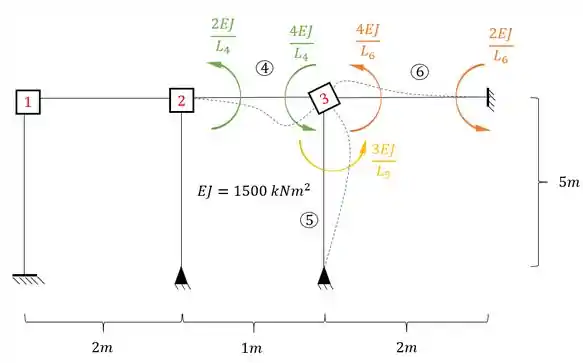
Juntando o que têm-se em cada nó, teremos que:
Passo 6
Organizando o sistema temos que:
Substituindo temos que:
Assim o nosso sistema será: