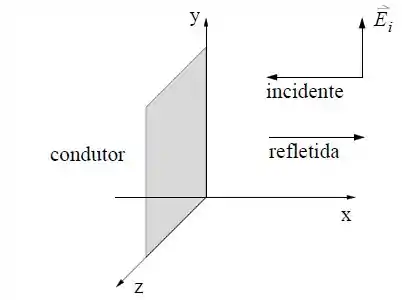
Uma onda eletromagnética plana monocromática com comprimento de onda , propagando-se no vácuo no sentido negativo do eixo , incide perpendicularmente sobre uma superfície metálica perfeitamente refletora, conforme a figura.
- Escreva a expressão do vetor campo elétrico incidente , em termos de sua amplitude e do comprimento de onda , sabendo que o campo oscila ao longo da direção e que assume seu valor máximo em no instante .
- Determine o vetor campo elétrico da onda refletida a partir do fato de que o campo elétrico total se anula na superfície do metal. Determine o vetor campo magnético da onda refletida a partir de .
- Calcule a pressão de radiação exercida pela onda sobre a superfície metálica perfeitamente refletora.
Determine o campo magnético da onda incidente a partir de ;
Passo 1
- Escreva a expressão do vetor campo elétrico incidente , em termos de sua amplitude e do comprimento de onda , sabendo que o campo oscila ao longo da direção e que assume seu valor máximo em no instante . Determine o campo magnético da onda incidente a partir de ;
- Determine o vetor campo elétrico da onda refletida a partir do fato de que o campo elétrico total se anula na superfície do metal. Determine o vetor campo magnético da onda refletida a partir de .
- Calcule a pressão de radiação exercida pela onda sobre a superfície metálica perfeitamente refletora.
Beleza! O problema já falou aqui que vai oscilar em ... isso significa que ele vai ter mais ou menos essa cara:
E isso bate com a informação de que quando e , .
A primeira dúvida que pode surgir aqui é o seguinte: como eu sei se o argumento dentro do cosseno é ou ?
O que pode ajudar é o seguinte: pensa que o cara que está dentro do cosseno tem que “permanecer constante”, certo? Então, como a onda está se deslocando na direção , está diminuindo... isso significa que, para que o argumento “permaneça constante”, o sinal deve ser positivo.
Por isso:
Passo 2
O próximo passo aqui é escrever esse cara como função de e ... isso significa que temos que escrever e em função de . Pra isso, basta usar as relações:
Agora podemos reescrever o campo elétrico como:
Passo 3
Agora vamos precisar relembrar algumas coisas... a primeira delas é que o campo magnético, o campo elétrico e a direção de propagação da onda são perpendiculares. Logo, se a onda se propaga no sentido e o campo elétrico se propaga no sentido , o campo magnético se propaga na direção ... só temos que saber se é no sentido ou .
Outro detalhe importante é que o produto vetorial vai apontar no sentido de propagação da onda... logo, só temos que ver qual dos dois vai resolver a nossa vida.
Logo, o campo magnético se propaga na direção . Isso significa que ele vai ter essa cara:
Pra finalizar, podemos escrever o como:
Finalmente:
Passo 4
Relaxa! A única coisa que muda aqui é o sentido de propagação da onda, então os argumentos dentro do cosseno também vão mudar...
Vamos fazer agora o mesmo que fizemos anteriormente... só que agora a onda vai se propagar no sentido . Pra que o argumento do cosseno “permaneça constante”, como aumenta e também aumenta, o argumento do cosseno deve ser:
Quando a onda é refletida:
Passo 5
Agora é o mesmo esquema de antes, para descobrir se o campo magnético está no sentido ou , temos que fazer o seguinte:
Então, como a onda agora se propaga no sentido , o campo magnético pode ser escrito como:
Passo 6
A pressão de radiação sobre uma superfície refletora é dada por:
Como varia com o tempo, o seu valor médio é dado por:
Resposta
a.
b.
c.