Uma onda eletromagnética plana e monocromática, com comprimento de onda , propaga-se no vácuo, no sentido negativo do eixo . A onda incide perpendicularmente sobre uma superfície condutora perfeita, conforme a figura abaixo.
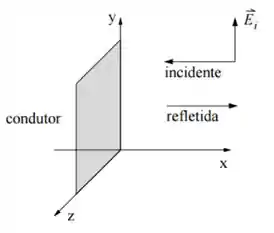
- Escreva a expressão do vetor campo elétrico incidente em termos de sua amplitude e do comprimento de onda , sabendo que o campo oscila ao longo da direção e assume seu valor máximo (positivo) em , no instante .
- Determine o campo magnético da onda incidente , a partir de .
- Determine o vetor campo elétrico da onda refletida , a partir do fato que o campo elétrico total se anula na superfície do metal.
- Determine o vetor campo magnético da onda refletida , a partir de .
- Calcule a pressão de radiação exercida pela onda sobre a superfície condutora perfeita.
Passo 1
Letra a)
Qual vai ser a expressão de ?
Bem, desconsiderando a direção, o campo elétrico é igual à sua amplitude multiplicada por uma função trigonométrica.
O argumento da função depende do sentido e direção de propagação da onda. Como nesse caso ela se propaga ao longo de (sentido negativo do eixo ), o argumento vai ser (Se acompanharmos uma frente de onda, quando o tempo passa, para esse argumento se manter constante é necessário que diminua).
A expressão então vai ser:
O motivo de ter o na expressão é porque não sabemos a fase do campo elétrico (ou seja, embora eu tenha posto a função “seno”, isso foi uma escolha totalmente arbitrária da minha parte).
Porém, sabemos que para e , o valor do campo elétrico é máximo. Então por um lado:
Mas por outro:
Igualando os dois, vemos que , o que implica que (equivalente a 90°). Nossa expressão fica:
Então se tivéssemos escolhido cosseno logo, já tava safo...
Por fim, a gente quer a expressão do vetor campo elétrico. Como ele vibra ao longo da direção (eixo ), temos:
E acabou, ufa! Calma aí, tão me chamando ali na produção... não acabou? AHN, ele queria tudo em função de !
Ok então gente, vamos lembrar de algumas relações pra ondas:
Pronto, agora sim!
Passo 2
Letra b)
Agora queremos o campo magnético. É, também acho que quem escreveu essa questão tinha que decidir de uma vez o que ele queria!
Mas tudo bem, porque pra achar o campo magnético, temos a nossa linda e maravilhosa expressão:
Que significa:
Agora só falta definir a direção de vibração de . Bem, ela é sempre perpendicular a , o que significa que definitivamente é ao longo do eixo (a outra opção era o eixo , mas luz não vibra na direção que ela tá indo, isso seria... sei lá, estranho).
Mas qual o sentido (da vida, o universo e tudo mais?)? Ou seja, está ao longo de ou de ?
O produto vetorial está na direção da propagação da onde. Usando a regra da mão direita, de estivesse vibrando ao longo de , a onda estaria indo pro sentido positivo do eixo .
Então, vibra de alegria ao longo de . EBA!
(Se você quiser, pode colocar o sinal de menos na frente da expressão toda, eu deixo.)
Passo 3
Letra c)
Qual a expressão do campo elétrico refletido ?
Bem, COMO EU VOU SABER ISSO? Acalme-se! Não vamos nos desesperar!
Ele diz que o campo elétrico total se anula na superfície do metal. Isso significa que:
Pra isso ser possível, eles precisam estar vibrando em sentidos opostos. Ou seja:
Como vibra na direção e sentido , então vibra na direção e sentido .
Por fim, ele segue na direção positiva do eixo , o que significa que o argumento na função trigonométrica passaria a ser
Logo, a sua expressão vai ser...
Só uma observação: Tem uma outra forma de enxergar a direção e sentido . Do que acabamos de falar em , temos que:
Ou seja, fazemos tudo do início, como antes, mas dessa vez considerando o argumento como sendo .
O que equivale a 270°. Acontece que:
Tá vendo? Eu disse que eu deixava você colocar o sinal do sentido de vibração na frente da expressão inteira!
Passo 4
Letra d)
Isso já tá ficando chato.
Vamos lá, as mesmas etapas:
Para a direção de vibração, é perpendicular a , logo ele vibra ao longo do eixo .
Como a onda está indo na direção positiva do eixo , então tem que ter o sentido de vibração como sendo o sentido negativo do eixo , que é . Logo:
Passo 5
Letra e)
A questão não nos disse se a superfície é um refletor perfeito ou um absorvedor perfeito. Mas ela nos disse que a superfície é um condutor perfeito.
Isso significa que ela é maravilhosa em conduzir eletricidade, e por isso as cargas na placa se afastam, e ficam todas na sua superfície.
Esse fato faz com que a placa condutora perfeita reflita a onda que acabamos de analisar (a onda refletida cancelando a onda incidente), evitando qualquer penetração da luz no material.
Se a luz não é absorvida, e a gente sabe que a luz é refletida... bem, isso me parece um refletor perfeito!
Ou seja, um condutor perfeito é também um refletor perfeito. (Sabe teu espelho? Esse aí que tu tem em casa? Então, quem reflete a luz tão bem é um sal de prata no fundo do vidro!)
Muito blá blá blá, mas o resultado é que:
Onde porque a superfície é um refletor perfeito e por causa da conservação do momento linear que a luz carrega.
Resposta
Letra a)
Letra b)
Letra c)
Letra d)
Letra e)