Num dado recipiente contendo um líquido, é imerso um cilindro contendo gás ideal, confinado por um êmbolo móvel, conforme as figuras adiante
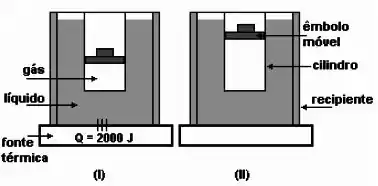
O recipiente está sobre uma fonte térmica e a base do recipiente é diatérmica, permitindo trocas de calor entre a fonte e o recipiente. As demais paredes do recipiente são adiabáticas e as paredes do cilindro que contém o gás são diatérmicas. A fonte térmica fornece 2000 J para o sistema formado pelo líquido e o gás, conforme figura (I) acima. Devido ao calor fornecido pela fonte térmica, a temperatura do líquido aumenta de 3K, consumindo 1500 J. Por outro lado, o gás realiza uma expansão com um aumento de volume de , a uma pressão constante de , como representado na figura (II) acima.
a) Calcule o trabalho realizado pelo gás.
b) Calcule a variação da energia interna do gás.
c) Nesse processo, o que acontece com a energia cinética das partículas que compõem o gás: aumenta, diminui ou não muda? Justifique a sua resposta.
Passo 1
a) O trabalho à pressão constante é calculado pela fórmula:
Passo 2
b) A energia interna do gás pode ser calculada pela 1ª lei da termodinâmica:
Como o calor cedido pela fonte é de 2000J e 1500J é absorvido pelo líquido, podemos concluir que 500J são absorvidos pelo gás!
Como o calor é absorvido, .
Passo 3
c) Como a energia interna aumenta, a temperatura aumenta e, consequentemente, a cinética das partículas também aumenta!
Se a variação de energia interna fosse negativa, a temperatura diminuiria e a velocidade das partículas também.
Resposta
a) -400J
b) 100J
c) A cinética das partículas aumenta!