A figura mostra duas forças de mesma magnitude agindo sobre um corpo. Se a magnitude comum das forças é e o ângulo é , que terceira força fará com que o corpo fique em equilíbrio.
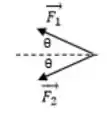
- apontando para a direita.
- apontando para a direita.
- apontando para a direita.
- apontando para a esquerda.
- apontanto para a esquerda.
Passo 1
Pensando no equilíbro, precisamos que a soma de todas as forças sobre o sistema seja nula, ou seja
Como temos 3 vetores o nosso problema será
E ainda podemos dividir essa equação em 2 fazendo a decomposição em e
Passo 2
Beleza! Mas quem são essas componentes? Pro vetor temos uma componente negativa (que aponta para esquerda) e uma componente positiva (que aponta para cima), assim
Pelo enunciado o módulo do vetor é , assim
Já pro vetor 2 temos algo parecido, só que a sua componente aponta para baixo
O enunciado nos conta que o módulo de também é , assim
Passo 3
Agora podemos voltar pras equações do passo 1!
Primeiramente na direção
Agora na direção
O nosso vetor então será
Isso aí é um vetor que aponta na direção positiva de , ou seja, é um vetor de módulo que aponta para direita!
Resposta
Letra a)