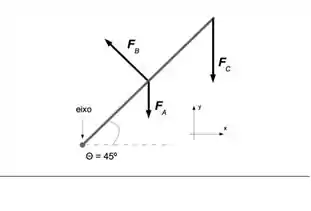
Uma haste, submetida às forças indicadas na figura, está presa a um eixo fixo em uma das suas extremidades. Sabendo-se que a haste pode girar livremente e que , podemos dizer que a resultante das forças que agem sobre a haste será zero se a força aplicada pelo eixo na haste for tal que:
(a) suas componentes e são ambas positivas.
(b) sua componentes e são ambas negativas.
(c) sua componente é nula e sua componente é igual à componente de .
(d) sua componente é positiva e sua componente é nula.
(e) sua componente é negativa e sua componente é antiparalela à componente de .
Passo 1
Precisamos descobrir o sentido das componentes e da força que será aplicada ao eixo para que a barra esteja em equilíbrio, pra isso vamos começar desenhando na barra essas componentes e também a decomposição da força .
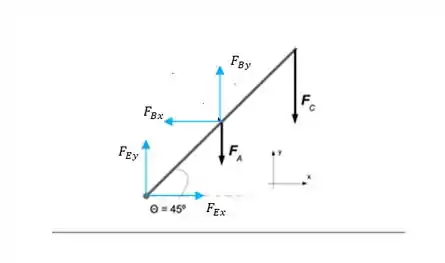
As componentes foram representadas com aquele sentido ali apenas para fazermos os cálculos, se por acaso encontrarmos sinais diferentes vamos trocar a direção das forças.
Com esse esquema da barra faremos o equilíbrio das forças nos eixos e , com as equações:
Passo 2
Vamos dar uma olhada pro eixo , pelo equilíbrio teríamos o seguinte:
Com isso a gente vê que o sentido do desenho foi adotado certo! Como só temos uma força em que é para a esquerda, a componente horizontal deve ser para a direita para equilibrar a barra.
Passo 3
Para o eixo faremos bem parecido, só fazer o equilíbrio das forças:
Po, mas e aí, tenho muitas incógnitas e não dá pra saber a direção de .
Lembra da condição que o enunciado nos deu? Vamos usar ela ali na nossa equação.
Ué, mas quem diabos é
Calma, é o nome carinhoso que o enunciado deu pro módulo da componente de . Vamos rearrumar essa equação toda pra um lado só da igualdade e jogar lá na equação do equilíbrio, ok?
Logo:
Poxa, mas lá em cima os valores não estão em módulo, podemos substituir mesmo assim? Lembra que o módulo retorna o valor absoluto?
Lá em cima temos a mesma configuração, é a mesma diferença em termos de valor absoluto sacou? Desse jeito podemos dizer que:
Então a equação anterior fica:
Então a componente também será positiva.
Resposta
(a)