Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Intervalo de Confiança para Proporção

Ver Todos os Exercícios

Teoria

Fala Aííí! Imagina comigo o seguinte cenário: Digamos que o reitor deseja estimar qual a proporção de estudantes da sua universidade que pratica esportes. Para isso, entrevistou uma amostra de 200 estudantes e verificou que 50 deles praticavam esportes. Se ele quiser construir um intervalo de confiança de 95 % para a proporção de esportistas da universidade, como ele pode fazer isso?

Vamos lá!! Para calcular o intervalo de confiança utilizamos a fórmula abaixo:

I C = p ^ - d ; p ^ + d

Tá... mas quem é p ^ e quem é d ?

Temos que p ^ é a nossa proporção amostral e podemos encontrar o seu valor da seguinte forma:

p ^ = 50   a l u n o s   q u e   p r a t i c a m   e s p o r t e s 200   a l u n o s   d a   a m o s t r a = 50   200   = 0,25

E d a nossa margem de erro que é dada por essa fórmulinha aqui:

d = z 1 - α 2 . p 1 - p n

Onde n   é o tamanho da amostra e p a média populacional. Beleza?!

Até agora está muito parecido com o que vimos nos tópicos anteriores, concorda?

Então vamos lá, nosso primeiro passo será encontrar o α . Dessa forma, teremos o nosso z 1 - α 2   para procurar na tabela da distribuição Normal, beleza?! Então como encontramos α ?

Utilizaremos o raciocínio

1 - α = n í v e l   d e   c o n f i a n ç a

Da mesma forma como fizemos nos tópicos anteriores.

Ou seja, no nosso problema, temos

1 - α = 0,95 → α = 0,05

Show de bola?!

Agora que temos o nosso α , conseguimos encontrar o nosso   z 1 - α 2 na tabela:

z 1 - α 2 = z 1 - 0,05 2 = z 0,975 → T a b e l a   N o r m a l → 1,96  

(Lembrando que para encontrar esse valor, nós procuramos na tabela normal qual o valor de Z que daria uma probabilidade de 0,975 e esse valor é Z = 1,96 .)

Opaaaa, então já temos uma parte do nosso d :

d = 1,96 . p 1 - p n

Se você reparar nós temos o valor de n = 200 então só falta o valor de p !

MAS PERAEEEE, O ENUNCIADO NÃO NOS DÁ O VALOR DE p... E AGORA?

Sempre que isso acontecer vamos ter duas opções:

  • Se no enunciado pedir um intervalo de confiança conservativo, podemos utilizar o valor máximo que p ( 1 - p ) pode assumir!

    • Mas beleza, que valor máximo é esse? Se você ainda não viu isso, o valor máximo que p ( 1 - p ) pode assumir é de 1 / 4 ou 0,25 , mas da onde vem isso? Se liga!

    Se você reparar bem, o valor de p está sempre entre 0 e 1 e quando multiplicamos ele pelo seu complementar ( 1 - p ) , nunca temos um valor acima de 0,25 .

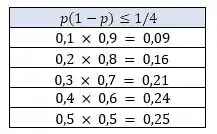
    Dessa forma, usando o valor máximo possível para p ( 1 - p ) , o numerador da raíz viraria 1 / 4 : d = 1,96 1 / 4   n = 1,96 1 / 4   200 = 0,07

    E com isso conseguimos calcular o nosso intervalo de confiança conservativo:

    I C = p ^ - d ; p ^ + d

    I C = 0,25 - 0,07 ; 0,25 + 0,07

    I C = ( 0,18 ; 0,32 )

    Beleza?!

  • Outra forma de fazer é utilizando a proporção amostral p ^ no lugar da proporção populacional p .

Quando fizermos isso, chamaremos o nosso intervalo de confiança de não-conservativo.

Nesse método o nosso d ficará da seguinte forma:

d = 1,96 . p ^ 1 - p ^ n

d = 1,96 . 0,25 1 - 0,25 200 = 0,06

E dessa forma conseguimos calcular o nosso intervalo de confiança não-conservativo:

I C = p ^ - d ; p ^ + d

I C = 0,25 - 0,06 ; 0,25 + 0,06

I C = 0,25 - 0,06 ; 0,25 + 0,06

I C = 0,22 ; 0,28

Show de bola?!

Dessa forma conseguimos calcular nossos intervalos de confiança que é o intervalo dentro do qual o nosso real valor do parâmetro está!

Nos vemos então nos exercícios!!

Exercícios Resolvidos

Exercício Resolvido #1

P2- 2012.2 – UFRJ Intervalo de Confiança

Um estudo com 420.095 dinamarqueses usuários de telefones celulares descobriu que 135 deles tinham desenvolvido câncer no cérebro. Uma pesquisa anterior a essa, diz que a taxa de incidência de tipo de câncer era de 0,034% para pessoas que não usavam telefones celulares.

  1. Construa um intervalo de 95% de confiança, não-conservativo, para a proporção de usuários de telefone celular que desenvolvem câncer no cérebro.

Passo 1

(a)

Nesse item a gente tem que montar um intervalo não-conservativo que tem essa cara aqui:

I C = p ^ - z 1 - α 2 . p ^ 1 - p ^ n   ;   p ^ + z 1 - α 2 . p ^ 1 - p ^ n

A gente pode calcular p ^ .

p ^ = 135 420095 = 0,000321

Passo 2

Pra gente montar o intervalo falta levar em consideração o 95%.

1 - α = 0,95 → α = 0,05

z 0,975 = 1,96

Agora a gente pode substituir no intervalo ali..

I C = 0,000321 - 1,96 × 0,000321 × 1 - 0,000321 420095   ;   0,000321 + 1,96 × 0,000321 × 1 - 0,000321 420095

I C = ( 0,000267   ;     0,000375 )

Resposta

a   I C = ( 0,000267   ;     0,000375 )

Exercício Resolvido #2

Lista Regina – CEFET Intervalo de Confiança

Um fabricante de calculadoras eletrônicas está interessado em estimar a fração de unidades defeituosas produzidas. Uma amostra aleatória de 800 calculadoras contém 10 defeitos. Calcule um intervalo de confiança de 99% para a fração defeituosa.

Passo 1

Note que vamos fazer um intervalo de confiança para uma fração, ou seja, I C para uma proporção.

Sabemos que vai ter essa cara aqui:

P p ^ - z 1 - α 2 . p ^ 1 - p ^ n ≤ p ≤ p ^ + z 1 - α 2 . p ^ 1 - p ^ n = 1 - α

Mas vamos com calma..

Passo 2

Confiança de 99%.

1 - α = 0,99

α = 0,01

e..

z 1 - α 2 = z 0,995

Olhando na tabela da Normal..

z 0,995 = 2,58

Passo 3

Calcular a estimativa amostral p ^ .

O problema diz que a amostra tem 800 calculadoras e 10 com defeito, então:

n = 800

p ^ = 10 800 = 0,0125

Passo 4

Agora só calcular...

P p ^ - z 1 - α 2 . p ^ 1 - p ^ n ≤ p ≤ p ^ + z 1 - α 2 . p ^ 1 - p ^ n = 1 - α

P 0,0125 - 2,58 × 0,0125 × 1 - 0,0125 800 ≤ p ≤ 0,0125 + 2,58 × 0,0125 × 1 - 0,0125 800 = 0,99

P 0,00238 ≤ p ≤ 0,0226 = 0,99

Assim:

I C = ( 0,00238   ; 0,0226 )

Resposta

P 0,00238 ≤ p ≤ 0,0226 = 0,99

Exercício Resolvido #3

Instituto de matemática UFRJ.

Pesquisadores desejam estudar o tempo gasto por engenheiros para executarem determinada tarefa. Para isto, foram selecionados aleatoriamente 64 engenheiros. Observou-se, nessa amostra, que a soma do tempo gasto por eles foi de 192 horas enquanto a soma dos quadrados dos tempos foi de 828 horas².

Sabendo-se que, dentre os 64 engenheiros selecionados, 16 eram recém formados, determine o intervalo de 99% de confiança (conservativo) para a proporção populacional de engenheiros recém formados.

Passo 1

(a)

Vamos anotar os dados que o problema deu..

n = 64

A gente sabe que o IC conservativo é da seguinte forma..

I C = p ^ - z 1 - α 2 . 1 4 n   ;   p ^ + z 1 - α 2 . 1 4 n

E de acordo com o problema,

p ^ = 16 64 = 0,25

Passo 2

Vamos calcular α e z 1 - α 2 .

1 - α = 0,99 → α = 0,01

z 1 - α 2 = z 0,995 = 2,57

Passo 3

Calculamos d ..

d = z 1 - α 2 . 1 4 n

d = 2,57 × 1 4 × 64

d = 0,16

Passo 4

Com isso temos nosso IC...

I C = 0,25 - 0,16   ; 0,25 + 0,16

I C = ( 0,09   ; 0,41 )

Resposta

I C = ( 0,09   ; 0,41 )

Exercício Resolvido #4

P2- 2013.1 – UFRJ Intervalo de Confiança

Os candidatos A e B disputam as eleições para a prefeitura da cidade de Bayesville. Em uma pesquisa de intenção de voto, uma amostra aleatória de tamanho 400 foi retirada da população e observou-se que a proporção dos eleitores que votariam em A era de 0,55 e a proporção dos eleitores que votariam em B era de 0,30, sendo o restante brancos, nulos e indecisos.

  1. Determine intervalos de 90% de confiança conservativos para a proporção de eleitores na população que votariam em A e para a proporção de eleitores na população que votariam em B, cada um deles com 3 casas decimais;
  2. Usando novamente a opção conservativa, qual deve ser o tamanho da amostra para que a margem de erro para cima ou para baixo da proporção amostral dos eleitores que votariam em A e da proporção amostral dos eleitores que votariam em B seja de 0,02 (ou de 2 pontos percentuais, usando a linguagem dos noticiários jornalísticos) com 95% de confiança?

Passo 1

(a)

Se liga, ele tá falando de intervalo de confiança conservativo. Se tu se lembrar, esse aqui é o intervalo conservativo..

I C = p ^ - z 1 - α 2 . 1 4 n   ;   p ^ + z 1 - α 2 . 1 4 n

Pros dois casos a gente tem algumas coisas em comum:

n = 400

1 - α = 0,9 → α = 0,1

z 0,95 = 1,64

A diferença é que para o candidato A   → p ^ = 0,55 e para o candidato B → p ^ = 0,30 . Então fica assim:

Para o candidato A:

I C = 0,55 - 1,64 × 1 1600   ; 0,55 + 1,64 × 1 1600

I C = 0,509   ; 0,591

Para o candidato B:

I C = 0,30 - 1,64 × 1 1600   ; 0,30 + 1,64 × 1 1600

I C = ( 0,259   ; 0,341 )

Passo 2

(b)

Essa margem que ele fala é exatamente o valor de d , concorda?

É esse valor z 1 - α 2 . 1 4 n que eles somam e diminuem de p ^ .

z 1 - α 2 . 1 4 n = 0,02

Porém agora..

1 - α = 0,95 → α = 0,05

z 0,975 = 1,96

Jogando isso ali na fórmula:

1,96 × 1 4 n = 0,02

n = 2401

Resposta

a   A → I C = 0,509   ; 0,591   ,   B → I C = ( 0,259   ; 0,341 )

b   n = 2401  

Exercício Resolvido #5

P2- 2012.1 – UFRJ - Intervalo de Confiança

Um grande banco deseja inferir sobre a proporção de clientes que estão satisfeitos com seu serviço. Para isto, entrevistou 25 clientes e obteve os resultados mostrados na seguinte lista:

SSISSISSSSSIISSSSSSISSSSS

em que S representa “cliente satisfeito” e I representa “cliente insatisfeito”.

  1. Construa um intervalo de confiança não conservativo ao nível de 96% para a proporção de clientes satisfeitos. O intervalo obtido contém a proporção de clientes satisfeitos?
  2. Qual deve ser o tamanho da amostra para que a amplitude do intervalo de confiança conservativo, ao nível de confiança de 98%, seja menor ou igual a 0,04?

Passo 1

(a)

Partiu construir um intervalo não-conservativo pra proporção. A gente sabe que a fórmula é a seguinte...

I C = p ^ - z 1 - α 2 . p ^ 1 - p ^ n   ;   p ^ + z 1 - α 2 . p ^ 1 - p ^ n

Pra isso então a gente precisa calcular algumas paradas.

Podemos calcular primeiro a proporção amostral dos clientes satisfeitos.

p ^ = 20 25 = 0,8

Passo 2

Ele diz que a confiança é de 96%, a gente sabe que isso quer dizer que:

1 - α = 0,96 → α - 0,04

z 0,98 = 2,05

Fiz isso procurando na tabela da Normal, dá uma olhada aí.

Passo 3

Agora é só jogar no intervalo e calcular...

I C = 0,8 - 2,05 × 0,8 × 0,2 25   ;   0,8 + 2,05 × 0,8 × 0,2 25

I C = ( 0,636   ; 0,964 )

O intervalo contem a proporção de 0,8 de clientes satisfeitos.

Passo 4

(b)

Primeiro vamos entender o que seria amplitude.

Amplitude seria a diferença entre os extremos do intervalo, correto?

Repara que se você fizer essa conta se vai descobrir que a amplitude é igual a duas vezes o valor de d .

Para um intervalo conservativo a gente sabe que é:

I C = p ^ - z 1 - α 2 . 1 4 n   ;   p ^ + z 1 - α 2 . 1 4 n

Ou seja,

d = z 1 - α 2 . 1 4 n

Passo 5

A gente tem que calcular n , sabendo que 2 d < 0,04 .

Primeiro vamos ver esse z aí.

1 - α = 0,98 → α = 0,02

z 0,99 = 2,33

Substituindo em 2 d < 0,04 .

2 × 2,33 × 1 2 n < 0,04

2,33 n < 0,04

n > 2,33 0,04 2

n = 3394

Resposta

a   I C = ( 0,636   ; 0,964 )

b   n = 3394

Exercícios de Livros Relacionados

A Associated Press (9 de outubro de 2002) relatou que em uma inspeção de 4722 jovens americanos, com idade entre 6 e 19 anos, 15% estavam seriamente acima do peso (índice de massa corporal de pelo men
Reconsidere o IC (7.10) para p e enfoque um nível de confiança de 95 % . Mostre que os limites de confiança estão de acordo com os do intervalo tradicional (7.11), uma vez que dois sucessos e duas fal
Uma de 56 amostras de algodão de pesquisa resultou em uma porcentagem de alongamento médio da amostra de 8,17 e desvio padrão amostral de 1,42 ("An Apparent Relation Between the Spiral Angle ϕ , the P
O artigo "Limited Yield Estimation for Visual Defect Sources" (IEEE Trans. on Semiconductor Manuf., 1997, p. 17-23) relatou que, em um estudo do processo de inspeção de um wafer específico, 356 dados
Uma amostra aleatória de 487 mulheres não-fumantes de peso normal (índice de massa corporal entre 19,8 e 26,0 ) que deram à luz em um grande centro médico metropolitano foi selecionada ("The Effects o