Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 10.Exercícios - Ex. 31

10-31. O gerente de uma frota de carros esta testando duas marcas de

pneus radiais. Elc coboca. ao acaso, um pueu de cada marca nas duas

rodas traseiras de oito carros e anda com ov carros alé que os pneus se

desgaslem. Os dados tem quilómetros) sao mostrados a seguir. Encon-

tre um intervalo de confianca de 9955 para a diferença na vida-média.

Baseado nos seus cáleulos. qual a marea que voce prefere?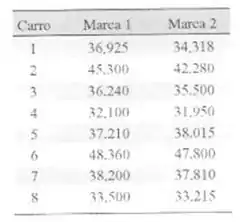

Passo 1

Oi oi gente,

Vamos lá fazer mais uma questão passo a passo?

Vem comigo!

Dados:

n = 8 c = 99 % = 0.99 ⇒ α = 1 - c = 1 - 0.99 = 0.01

Determine a diferença no valor de cada par.

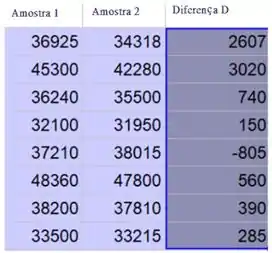
Passo 2

Determine a média da amostra das diferenças:

d - = 2607 + 3020 + … + 390 + 285 8 ≈ 868.375

Determine o desvio padrão da amostra das diferenças:

s d = ( 2607 - 868.375 ) 2 + … + ( 285 - 868.375 ) 2 8 - 1 ≈ 1290.0331

Determine o t α / 2 usando a tabela V com d f = n - 1 = 8 - 1 = 7 :

t 0.005 = 3.499

Os pontos finais do intervalo de confiança são:

d - - t α 2 ⋅ s d n = 868.375 - 3.499 ⋅ 1290.0331 8 ≈ - 727.503 d - + t α / 2 ⋅ s d n = 868.375 + 3.499 ⋅ 1290.0331 8 ≈ 2464.253

Eu não preferiria nenhuma das marcas, porque o intervalo de confiança contém 0, o que indica que é provável que a vida média seja a mesma para ambas as marcas.

Resposta

- 727.503 < μ d < 2464.253

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a. Use a fórmula geral da variância de uma combinação linear para escrever uma expressão para V ( a X + Y ) . Então, seja a = σ Y / σ X , e mostre que p ≥ - 1 . [Sugestão: a variância sempre é ≥ 0 , e
Se a quantidade de refrigerante que consumo em certo dia é independente do consumo em qualquer outro dia e é normalmente distribuída com μ = 13 oz e σ = 2 , e se eu atualmente tenho duas caixas com se
a. Mostre que C o v X ,Y + Z = C o v X ,Y + C o v ( X ,Z ) . b. Sejam X 1 e X 2 as pontuações verbal e quantitativa em um exame de aptidão, e Y 1 e Y 2 as pontuações correspondentes em outro exame. Se
Suponha que a proporção de eleitores rurais em um determinado estado que favorece certo candidato a governador seja de 0,45 e que a proporção de eleitores urbanos e suburbanos que o favorecem seja de
Suponha que a pontuação verbal X e a pontuação quantitativa Y de um indivíduo escolhido aleatoriamente em um exame de aptidão administrado nacionalmente tenham fdp conjunta. f x , y = 2 5 2 x + 3 y0 ≤