Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 10.Exercícios - Ex. 9
10-9. Pensa-se que a concentração de um ingrediente ativo em um detergente liquido para lavagen de roupas seja afetada pelo tipo de cataIsador usado no processo. O dessio-padrao da concentraçào ativa e 3 gramas por litro, independentemente do tipo de catalisador. Dez observações na concentração são feitas com cada catalisador, sendo os dados mostrados a seguir:
Catalisador 1:57.9. 66.2. 65.4, 65.4. 65.2. 62.6. 67.6. 63.7. 67.2. 71.0
Catalisador 2: 66,4, 71.7. 70.3.69.3, 64,8, 69.6, 68.6, 69,4, 65.3, 68.8
(a) Encontre um intervalo de confiança de 95 para a diferença de concentraçoes medias ativas para os dois catalisadons Encontne o valor P.
(b) Há alguma evidencia ndicando qu as concentraçoes medias ativas dependem da escolha do catalisador! Baseie a sua resposta nos resultados do item a).
(c) Suponha que a diferença média verdadeira na concentraço ativa seja 5 gramas por litro. Qual é a poténcia do testle para detectar essa diferença se a - (0,05?
(d) Se essa diferença de 5 gramas por litro for realmente importante voce considena adequados os tamanhos das amostras usads pelo experimentalista? A suposição de normalidade parece razoável para ambas as anmostras?
Passo 1
Oi oi gente, tudo bom com vocês?
Vamos fazer essa questão aqui de um jeito bem passo a passo pra facilitar a vida de todo mundo!Boraaa
Dados:
A média é a soma de todas os valores dividida pelo número de valores:
Passo 2
Letra a:
Para o nível de confiança , determine usando a tabela de probabilidade normal no apêndice (procure 0.025 na tabela, o valor z é então o valor z encontrado com o sinal oposto):
Os pontos finais do intervalo de confiança para são:
Determine o valor da estatística de teste:
O valor P é a probabilidade de obter um valor mais extremo ou igual à estatística de teste padronizada z. Determine a probabilidade usando a tabela III.
Passo 3
Letra b:
Há evidências suficientes para apoiar a alegação de que as concentrações ativas médias dependem da escolha dos catalisadores, porque o valor P é pequeno e o intervalo de confiança não contém 0.
Passo 4
Letra c:
A potência é a probabilidade de rejeitar a hipótese nula quando a hipótese alternativa for verdadeira.
Determine o valor z correspondente a uma probabilidade de :
A diferença média da amostra correspondente é a diferença média da população (da hipótese) aumentada pelo produto do valor z e o desvio padrão:
O valor z é a diferença média da amostra diminuída pela diferença média da população (diferença da média alternativa!) dividido pelo desvio padrão:
Determine a probabilidade de rejeitar a hipótese nula usando a tabela III:
Passo 5
Letra d:
Os tamanhos das amostras parecem ser adequados, porque o intervalo de confiança da parte (a) continha -5 e, portanto, a média diferente de 5 foi detectada (neste caso).
Para verificar a normalidade, criaremos dois gráficos de probabilidade normal para ambos os conjuntos de dados.
Gráfico de Probabilidade Normal:
Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.
Se os dados contém n valores de dados, então as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) em relação a .
A menor pontuação padronizada corresponde ao menor valor de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.
Passo 6
Catalisador 1:
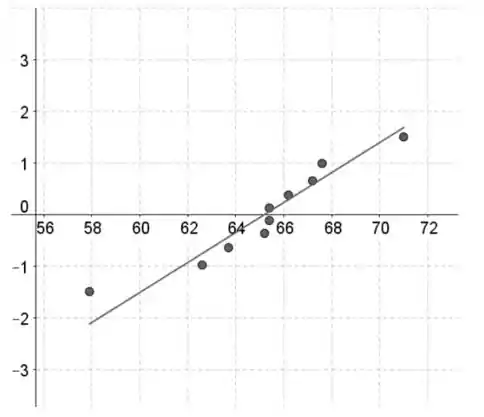
Catalisador 2:
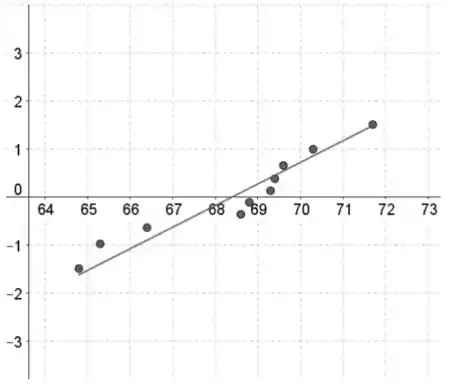
A suposição normal parece ser razoável para ambas as amostras, porque ambos os gráficos de probabilidade normal não contêm curvatura forte e parecem ser aproximadamente simétricos.
Resposta
- Há evidências suficientes para apoiar a alegação de que as concentrações ativas médias dependem da escolha dos catalisadores, porque o valor P é pequeno e o intervalo de confiança não contém 0.
- Tamanhos de amostra adequados, a suposição normal é razoável