10-10. Considere o teste de hipóteses Suponha que os tamanhos de amostra sejam n, = 15 e que os dados sejam retirados de distribuições normais.Use a

(a) Teste a hipxitese e encontre o valor P.

(b) Explique como o teste paxderia ser conduzido com um intervalo de confiança.

(c) Qual é a poténcia do teste no item (a) para uma diferença verdadeira de médias igual a 3?

(d) Considerando tamanhos iguais de amostras, que tamanho de amostra deveria ser usado para obter B- 0,05, se a diferença verdadeira de médias fosse -2?

Letra a:

A estatística é

Onde

Então

Como , encontramos na Tabela V do Apêndice que

Portanto, concluímos que o limite superior do valor P é

Portanto, como o valor P é menor que , rejeitamos .

Letra b:

Um intervalo de confiança de na diferença nas médias é

Sabemos que . Portanto, do Apêndice Tabela V, obtemos

Portanto, um IC de 95% na diferença de médias é

Observe que o intervalo de confiança de 95% não inclui zero. Portanto, neste nível de confiança concluímos que existe uma diferença nas médias.

Letra c:

Para o teste bilateral quando e, usamos os Gráficos VIIe e VIIf com

onde é a verdadeira diferença nos meios que interessam. Para usar essas curvas. devemos ser inseridos com o tamanho da amostra . Sabemos que e . Usando como uma estimativa grosseira do desvio padrão comum , temos

E

Do Gráfico do Apêndice VIIe com e encontramos (veja a próxima figura, linha vermelha).

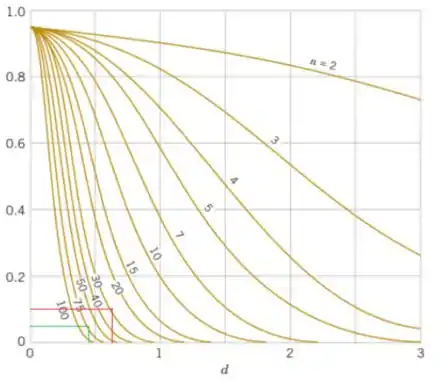
Então, a potência do teste na parte a) é

Letra d:

Agora, usamos e a verdadeira diferença nas médias .

Portanto,

Do Apêndice Gráfico VIIe com e , encontramos (ver figura anterior, linha verde).

Portanto, como

e usaríamos tamanhos de amostra de