Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 13
11-13. Um artigo no Jourmal of Envirommenial Engineering Dvision Lrast Squares Estimates of BOD Parameters - Estimativas de
Minimos Quadrados dos Parâmetros de DBO". 1980. Vol. 106. pp.
1197-12021 tomou uma amostra do rio Holston abaixo de Kingport.
Tennessee. durante o mês de agosto de 1977. O teste de demanla bio-
química de oxigênin (DBO) é conduzido durante um periodo de tempo
dado em dias. Os dados resultantes são mostralos a seguir:
a)Considerando que um modelo de regressão lincar seja apropriado.
ajuste o modelo de regressão relacionando DBO (y) com o tempo x. Qual é a estimativa de
b) Qual é a cstimativa do nivel esperado de DBO para um tempo de 15
dias?
c) Que variação no DBO médio é esperado quando o tempo varia por
3 dias?
d)Suponha que o tempo usado seja 6 dias. Calcule o valor ajustado de
ye o residuo correspondente.
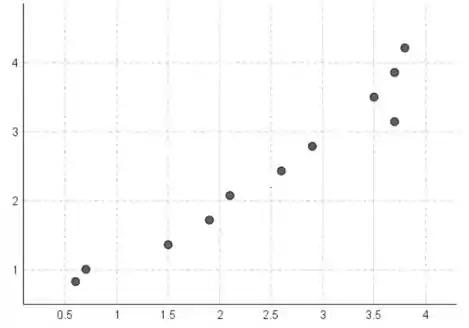
e) Calcule ajustado para cada valor de x, usado para ajustar o mode-
lo. Construa então um gráfico de ý verstus os valores observados cor
respondentes y, e comente o que esse gráfico pareceria se a relaçào
entre ve x fosse uma linha reta deterministica (nenhum erro aleató-
rio). O gráfico obtido realmente indica que o lempo é uma variável
regressora efetiva na previsão de DBO?
Passo 1
Oi oi gente,
Vamos lá fazer mais uma questão passo a passo?
Vem comigo!
Dados:
Letra a:
As estimativas de mínimos quadrados da interceptação e inclinação são:
A linha de regressão de mínimos quadrados torna-se então:
Determine a soma dos erros quadrados:
é então estimado pela soma dos erros quadráticos divididos pelo tamanho da amostra diminuída por 2:
Passo 2
Letra b:
Substitua x na linha de regressão de mínimos quadrados por 15 e avalie:
Passo 3
Letra c:
Substitua x na linha de regressão de mínimos quadrados por 3 e avalie:
Passo 4
Letra d:
Substitua x na linha de regressão de mínimos quadrados por 6 e avalie:
O resíduo é o valor real diminuído pelo valor previsto:
Passo 5
Letra e:
Os valores y estão no eixo horizontal e os valores ajustados estão no eixo vertical.
Resposta
- Sim