Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 11.Exercícios - Ex. 88
11-88. Atomos de césio. resfriados por laser. poderiam ser usados para
construir relógios atômicos baratos. Em um estudo em IEEE Transac-
tions on Instrumentation and Measurement (2001. Vol. 50. pp. 1224
1228), o número de átomos resfriados por lasers de várias poténcias foi
contado.
a) Faça um gráfico dos dados e ajuste uma linha de regressão para pre-
ver o número de átomos provenientes de uma fonte de laser. Comente
a adequação de um moxielo linear.
b) Há uma regressáos significativa. com a - 0.05? Qual é o valor P?
c) Estime o coeficiente de correlação.
d) Teste a hipótese que p = 0 contra a aliernativa p =0.-0.05.
Qual é o valor P?
e) Calcule um intervalo de confiança de 955% para o coeficiente de in-
clinacão.
Passo 1
Faaaaaaala aí gente,
Vamos fazer uma daquelas questões passo a passo?
Vem comigo!!
Vamos denotar a variável de quilate com a letra x, e a variável aleatória de preço com a letra y. Então, depois de processar os dados fornecidos na tabela chegamos ao seguinte gráfico de dispersão dos dados:
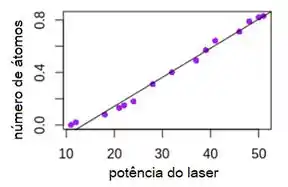
Na imagem acima, também apresentamos o ajuste linear aos dados.
Aqui estão as etapas para obter este modelo para que você possa verificar seu trabalho (nota que ):
Agora estamos prontos para determinar os coeficientes do modelo:
Portanto, o melhor ajuste linear para os dados é:
O ajuste parece ótimo e o modelo linear parece adequado, por exemplo, o coeficiente de determinação é enorme:
Passo 2
Letra b:
Precisamos testar a significância da regressão. Neste exercício, vamos optar pela abordagem de análise de variância para este problema. Primeiro, avalie a regressão e a soma dos quadrados dos erros:
para calcular o valor da estatística F:
Rejeitamos então rejeite por causa da enorme estatística de teste que obtivemos.
Portanto, o modelo é significativo.
O valor p é aproximadamente 0.
Passo 3
Letra c e d:
Calcule (ou obtenha do software) a estimativa do coeficiente de correlação:
Agora, teste para a hipótese nula de com a alternativa bilateral.
Calcule a estatística de teste:
e concluímos que rejeitamos a hipótese nula de em favor da alternativa de dois lados porque .
O valor p é .
Passo 4
Letra e:
O intervalo de confiança da inclinação é dado pela seguinte fórmula:
Portanto, calculamos:
E obtemos:
Resposta
- , o modelo é significativo, valor de p aproximadamente 0
- , o valor P é aproximadamente 0