11-87. Pensa-se que os gramas de sólidos removidos de um material (y)
eslejam relacionados ao tempo de secagem. Dez observações obtidas a
partir de um estudo experimental sâo dadas a seguir:

a)Construa um diagrama de dispersão para esses dados.
b) Ajuste um modelo de regressão linear simples a esses dados.
c) Teste a significancia da regressão.
d) Baseando-se nesses dados. qual é sua estimativa dos gramas médios
de sólidos removidos em 4.25 horas? Encontre um intervalo de con-
fianca de 95'5 para a média.
e) Analise os residuos e comente a adequação do modelo.
Passo 1
Faaaaaaala aí gente,
Vamos fazer uma daquelas questões passo a passo?
Vem comigo!!
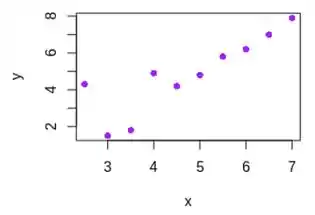
Letra a:
Depois de processar os dados, chegamos ao seguinte gráfico de dispersão:
Passo 2
Letra b:
Primeiro, vamos calcular as quantidades importantes (nota que .
Agora estamos prontos para determinar os coeficientes do modelo:
Portanto, o melhor ajuste linear para os dados é:
Passo 3
Letra c:
Precisamos testar a significância da regressão. Neste exercício, vamos optar pela abordagem de análise de variância para este problema.
Primeiro, avalie a regressão e a soma dos quadrados dos erros:
para calcular o valor da estatística F:
Rejeitamos então primeiro, vamos determinar:
e então rejeitar
Portanto, o modelo é significativo.
Passo 4
Letra d:
Vamos lembrar que o significado do modelo de regressão é a seguinte relação:
Podemos estimar os parâmetros para obter a estimativa pontual desta expectativa condicional (resposta da média):
Agora lembre-se da fórmula para o intervalo de confiança de na resposta da média em:
Agora calcule as quantidades necessárias a partir dos dados (ou use já calculado) para encontrar:
Passo 5
Letra e:
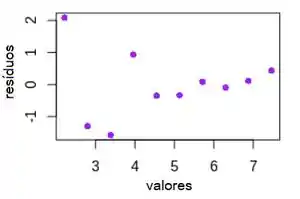
Plote os resíduos do modelo em relação aos valores ajustados para a resposta e examine o gráfico.
Concluímos que a variância não é a mesma em todo o intervalo dos dados, porque os resíduos são muito menores para os maiores valores ajustados.
Portanto, o modelo não é totalmente adequado.
Resposta
- Olhar resolução
- , o modelo é significativo
- Ver resolução