Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 12.Exercícios - Ex. 60
12-60. Conskkere o modelo de regressão para os dados de escapamento
cdo Exereício 12 14.
a) Que proporcao da variabilidade total é explicada por esse modelo?
b)Comstrua um grático de probabilidade normal dos nesiduos. Que
conelusao voce pode tirar desse gratico?
c) Plote os residuos contra ve contra cada regressor e comente a ade
quação do moxlelo.
d)Caleule a distância Cook para as observaçües nesse conjunto de
dados. Existe alguma observação influente nesses dados?
Passo 1
Faaaala ai gente, tudo bom?
Vamos resolver essa questão aqui rapidinho?
Bora, é tranquilo
Neste exercício, você deve usar os dados fornecidos no exercício 12.14.
Letra a:
Para calcular o coeficiente de determinação-precisam ser obtidos. Portanto:
Finalmente,
que cerca de 91,36% da variabilidade total é explicada pelo modelo.
Passo 2
Letra b:
Agora traçamos o gráfico de probabilidade normal para os resíduos (abaixo). Vemos que a suposição de normalidade é razoavelmente justificada.
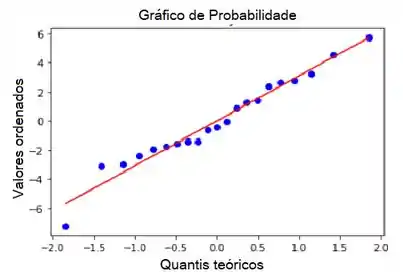
Passo 3
Letra c:
Agora representamos os resíduos em relação a todos os regressores e em relação às previsões do modelo. Concluímos que o modelo é adequado, (dispersão geralmente aleatória em torno de y = 0).
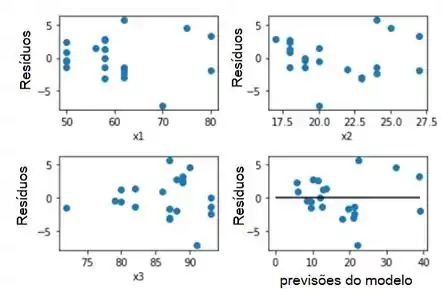
Passo 4
Letra d:
Calcule a distância de Cook para todas as observações de acordo com a fórmula:
onde resíduo, e k=3 número de variáveis.
Nenhuma observação foi considerada influente.
Resposta
- Ver resolução
- Ver resolução
- Nenhuma observação foi considerada influente.