Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 13.Exercícios propostos - Ex. 3a
Os dados da tabela referem-se a um grupo de 11 casas alugadas:
Pede-se:
- Elaborar a regressão linear dos aluguéis sobre as idades das casas.
Passo 1
Olá galerinha, tudo bem com vocês? Primeiramente iremos relembrar a teoria.
O método dos mínimos quadrados é um dos métodos utilizados para estimar os parâmetros da regressão. Onde iremos estimar os parâmetros e da reta da regressão, e chamaremos de e , respectivamente. Sendo assim:
- reta de regressão de sobre ;
- estimativa da reta de regressão.
O método dos mínimos quadrados fornece os valores de e tais que seja mínimo. Iremos descobrir os valores de e pela Regra de Cramer. Para isso, iremos utilizar algumas equações:
- Os valores médios de e :
- As variâncias são calculadas pelas seguintes equações:
- E as estimativas procuradas de e :
- idade;
- aluguel.
Passo 2
Sendo assim, iremos iniciar nosso exercício, onde iremos considerar:
Agora vamos calcular os valores de , e , para isso iremos construir a tabela:
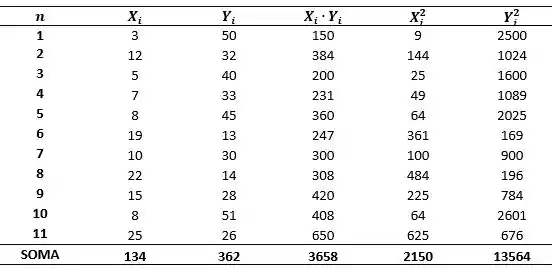
Passo 2
Vamos calcular a média de e :
Passo 3
E por fim, iremos obter os valores de e , para obtermos a equação da reta:
Sendo assim:
Prontinho pessoal, até mais!
Resposta
.