Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 12.Exercícios - Ex. 91
12-91. Considere os dados do inversor do Exercicio 12-90. Remova a
observação 2 dos dados originais. Defina as novas variávcis como se
segue
a) Ajuste a modelo de regressão usando esses regressores transforma-
dos (não iuse x).
b)Teste o modelo para a signitieincia da regressåo usando a = 0.05.
Use o teste t para investigar a contribuicão de cada variável ao mo
delo ( 0.05). Quais sáo as suas conelusies?
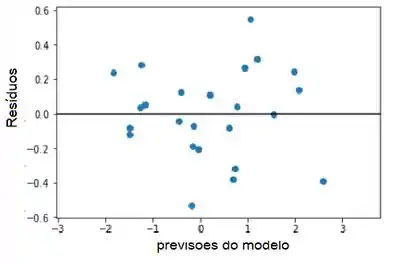
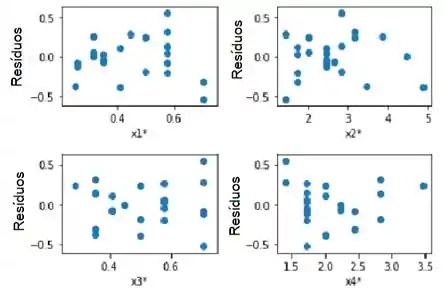
c) Plote os resíduos contra y' e contra cada um dos regressores trans-
formados. Comente esses gráficos.
Passo 1
Faaaala ai gente, tudo bom?
Vamos resolver essa questão aqui rapidinho?
Bora, é tranquilo
Letra a:
Ajuste o modelo linear usando os regressores e transformações mencionados:
Passo 2
Letra b:
A estatística de teste F deve ser calculada como segue.
Sabemos que:
Vamos lembrar que:
E então:
Agora, vamos calcular:
Portanto, a estatística F é
O valor P para o teste de significância da regressão é então obtido como
A hipótese é, portanto, rejeitada e a regressão é significativa.
Passo 3
Nós precisamos calcular as estatísticas de teste para os coeficientes de regressão de . Calcule
Os valores de p correspondentes para testes t são então facilmente obtidos e todos são muito pequenos (aproximadamente 0).
Portanto, a hipótese nula de os coeficientes serem 0 é rejeitada (sob para todas as variáveis no modelo.
Passo 4
Letra c:
Agora apresentamos os gráficos de resíduos versus previsões e regressores. Observamos que todas as parcelas estão perfeitas!
Resposta
- Rejeite as hipóteses nulas para todos os testes. Todos os valores de p são muito pequenos. O modelo e todos os regressores são significantes sob
- Os gráficos são perfeitos.