12-90. Os pontos transientes de um inversor eletrônico são intluencia-
dos por muitos lalores. A Tabcla 12-22 apresenta os dados sobre o pon
to transiente (y. em voltsi dos inversores PMOS-NMOS ecinco regres-
sores candidatos: x,-largura do dispositivo NMOS.x.-comprimen-
to do dispositivo NMOS. x, = largura do dispositivo PMOS.x,-com-
primento do dispositivo PMOS e x, = temperatura (℃).
a) Ajuste o modelo de regressão lincar miltipla a esses dados. usando
lolos os regressores. Teste a significancia da regressão usando a=
0.01.Enconire o valor P para esse teste e usc-o para tirar suas con
clusoes.
b)Teste a contribuição de cada variável ao modelo. usando o teste t.
com x = 0,05. Quais são as suas conclusoes?
c)Remova x, do modclo. Teste o novo modelo com relação à signifi.
cáncia da regressão. Tesle também. com o teste t. a contribuição
relativa de cada regressor para o novo moxdelo. Usando « - 0.05,
quais são as suas conclusoes?
d) Note que a MQ, para o modelo no item (c) é menor do que a MQ,
para o modelo completo no item (a). Explique por quc isso ocorreu.
e) Calcule os residuos na forma de Student. Algum desses resíduos
parece excepcionalmente grande?
f) Suponha que vocé descubra que a segunda observacão estava regis-
trakda incorretamente. Remova essa observação e reajusle o modelo
usando.xi. x2.x, e t, como regressores. Note que R para esse mode-
lo é consideravelmente maior do que Ri para os modelos ajustados
previamente. Explique por que o R- para esse modelo aumentou.
g) Teste o modclo do item (fi com relação à significáncia da regressão
usando a - 0.05. Investigue também a contribuição de cada regres-
sor para o imodelo, usando o teste t com u-0.05. Que conclusões
voce pode tirur?
h) Plote os residuos do modelo no item (f) contra ý e contra cada um
dos regressores. Comente esses gráficos.
Passo 1
Faaaala ai gente, tudo bom?
Vamos resolver essa questão aqui rapidinho?
Bora, é tranquilo
Letra a:
Eu ajustei o modelo linear usando os 5 regressores mencionados:
Sabemos que a estatística de teste F deve ser calculada da seguinte maneira.
Nós sabemos que:
Vamos lembrar que:
Então,
Portanto, a estatística F é
O valor p para o teste de significância da regressão é então obtido como
A hipótese é, portanto, rejeitada, a regressão é significativa.
Passo 2
Letra b:
Precisamos calcular as estatísticas de teste para os coeficientes de regressão até .
Calcule:
Os valores p correspondentes para os testes t são então facilmente obtidos:
Portanto, a hipótese nula do coeficiente ser 0 é rejeitada (sob , para todas as variáveis, exceto , o que não contribui para o modelo
Passo 3
Letra c:
Vamos excluir do modelo melhora o modelo.
Nós facilmente recalculamos as quantidades, por exemplo
Vamos recalcular facilmente as quantidades, por exemplo
e determinar a estatística F:
e o valor p para o teste de significância
e concluímos que rejeitamos a hipótese nula de regressão insignificante.
Além disso, os testes t para coeficientes individuais resultam em rejeições de hipóteses nulas.
Passo 4
Letra d:
Calcule para ambos os modelos:
Embora o modelo completo tenha um erro residual , ligeiramente menor, o segundo modelo tem melhor (menor) devido a uma variável a menos! Os modelos explicam uma quantidade muito semelhante de variabilidade, mas o segundo modelo é mais simples.
Passo 5
Letra e:
De todos os resíduos um é extraordinariamente grande, aquele referente à segunda medição:
Passo 6
Letra f:
O novo modelo (sem usar a segunda observação) é dado como:
Calcule o coeficiente de determinação:
Agora, quando não há um outlier significativo como é o caso com a segunda observação, o modelo explica melhor os dados.
Passo 7
Letra g:
Excluindo a segunda observação do modelo melhora o modelo.
Nós facilmente recalculamos as quantidades, por exemplo
e determine a estatística F:
e o valor p para o teste de significância
e concluímos que rejeitamos a hipótese nula de regressão insignificante.
Além disso, os testes t para coeficientes individuais resultam em rejeições de hipóteses nulas.
Passo 8
Letra h:
Agora apresentamos os gráficos de resíduos versus previsões e todos os regressores (modelo final). Os gráficos sugerem de certa forma não linearidade e variância não homogênea:
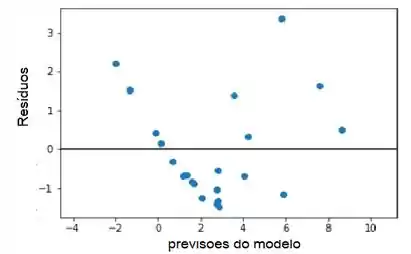
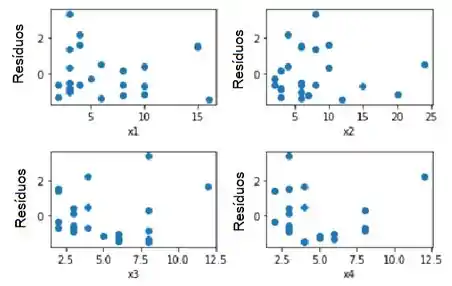
Resposta
- , Rejeita
- A hipótese nula do coeficiente ser 0 é rejeitada (sob , para todas as variáveis, exceto , o que não contribui para o modelo
- O novo modelo é melhor. A estatística de teste para o teste de significância é
- MSE ligeiramente inferior do novo modelo,
- A segunda observação é estranha, com o resíduo de
- Novo modelo:
- Este novo modelo é o melhor, estatística de teste: e valor p minúsculo.
O novo modelo tem um muito maior com porque a segunda observação não foi bem explicada pelo modelo anterior.