Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 35
Como a aceleração lateral – forças laterais experimentadas em viagens que em grande medida podem ser controladas pelo motorista – influencia na náusea sentida por passageiros de ônibus? O artigo "Motion Sickness in Public Road Transport: The Effect of Driver, Route, and Vehicle" (Ergonomics, 1999, p. 1646–1664) apresentou dados sobre x quantidade de náusea de movimento (calculada de acordo com um padrão britânico para avaliar movimentos semelhantes no mar) e y náusea relatada (%). As quantidades pertinentes são
Os valores da quantidade na amostra estão entre 6,0 e 17,6. a. Supondo que o modelo de regressão linear simples seja válido para relacionar essas duas variáveis (isso é confirmado pelos dados brutos), calcule e interprete uma estimativa do parâmetro do coeficiente angular que transmita informações sobre a precisão e a confiabilidade da estimativa. b. Parece haver uma relação linear útil entre essas duas variáveis? Responda à pergunta, empregando a abordagem do valor P. c. Seria sensato usar o modelo de regressão linear simples como base para prever a porcentagem de náusea quando a quantidade 5,0? Explique seu raciocínio. d. Quando o MINITAB foi usado para ajustar o modelo de regressão linear simples aos dados brutos, foi indicado que a observação (6,0, 2,50) possivelmente tivesse um impacto significativo sobre o ajuste. Elimine essa observação da amostra e recalcule a estimativesse da parte (a). Com base nisso, a obser
Passo 1
Usaremos o seguinte:
Regressão linear é uma equação linear de duas variáveis das quais uma é independente e uma é dependente da outra. Seja X uma variável independente e Y dependente. Do que a equação linear é definida por
Onde são coeficientes. E a fórmula para calcular esses coeficientes é a seguinte:
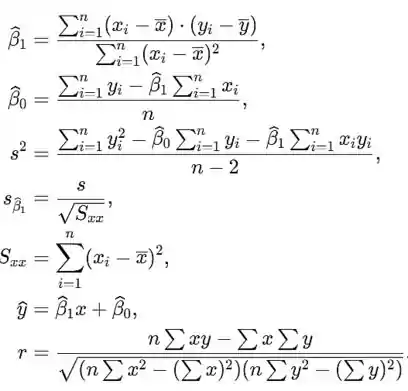
E o teste de utilidade do modelo é dado por:
Com t estatístico
Nesta tarefa, temos dados sobre a dose de enjoo (x) e a náusea relatada (y). Os dados são dados abaixo:
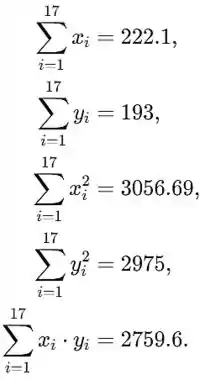
Passo 2
- Nesta subseção precisamos calcular a inclinação Temos a seguir
- Se quisermos testar se este modelo é útil ou não, precisamos testar hipóteses:
- Podemos prever % náusea para a dose 5, mas talvez não obtenhamos o valor mais preciso porque esse modelo usamos para valor entre 6 e 17,6. Mas o valor previsto é dado abaixo:
- Agora vamos excluir o ponto (6,2.5). Agora temos o seguinte:
O coeficiente de inclinação é igual a -8.71
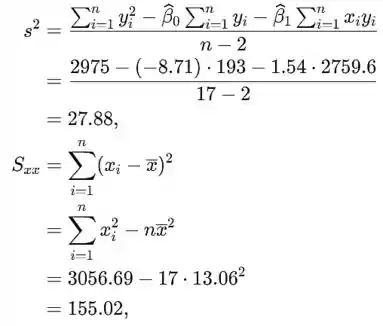
Como o valor de p é menor que 0.01 significa que rejeitamos hipóteses nulas e aceitamos alternativas. Então, este modelo é bom para previsão.
Passo 3
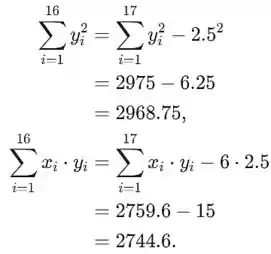
Agora o novo modelo sem usar o ponto (6,2.5) é dado por:
Resposta
Respondemos a todas as perguntas nesta tarefa.