Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 36
Uma névoa (gotículas transportadas pelo ar ou aerossóis) é gerada quando fluidos para remoção de metal são usados em operações de máquina para resfriar e lubrificar a ferramenta e a peça. A produção de névoa é uma preocupação para a Occupational Safety and Health Administration (OSHA), que recentemente diminuiu substancialmente o nível nos locais de trabalho. O artigo "Variables Affecting Mist Generation from Metal Removal Fluids" (Lubrication Engr., 2002, p. 10–17) apresentou os dados a seguir sobre x velocidade do fluxo do fluido para um óleo 5% solúvel (cm/s) e y a quantidade de gotículas de névoa com diâmetro menor que 10 m (mg/m3 ):
a. Os pesquisadores executaram uma análise de regressão linear simples para relacionar as duas variáveis. O gráfico de dispersão dos dados apóia essa estratégia? b. Que proporção da variação observada no volume de névoa pode ser atribuída à relação de regressão linear simples entre velocidade e névoa? c. Os investigadores estavam particularmente interessados no impacto sobre a névoa ao aumentar a velocidade de 100 para 1000 (um fator de 10 correspondente à diferença entre o menor e o maior valores x na amostra). Quando x aumenta dessa forma, há alguma evidência significativa de que o aumento médio real em y é menor que 0,6? d. Estime a mudança média real na névoa associada com um aumento de velocidade de 1 cm/s. Faça isso de maneira que transmita informações sobre precisão e confiança.
Passo 1
- x está no eixo horizontal e y está no eixo vertical
- Determine a equação de regressão dos mínimos quadrados
- Determine a diferença dos valores y que correspondem ao valor x mais baixo e mais alto:
- Vamos calcular um intervalo de confiança de 95%, outros níveis de confiança podem ser determinados de forma semelhante:
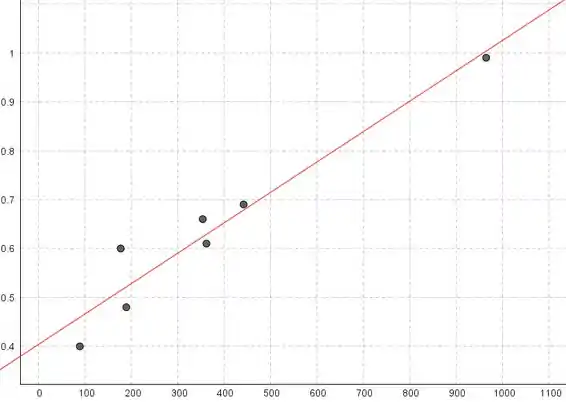
Um gráfico de dispersão dos dados suporta a estratégia de uma análise de regressão linear simples, porque o gráfico de dispersão não contém curvatura forte e o padrão no gráfico de dispersão é aproximadamente linear.
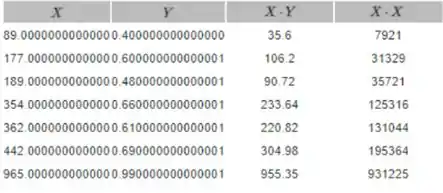
Encontrando a soma de todas as colunas
Usando as seguintes equações para encontrar a e b:
Substituindo a e b na equação de regressão
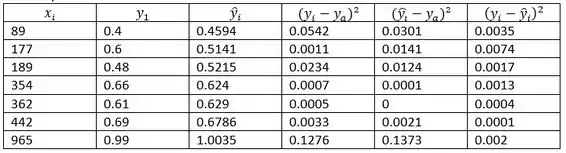
Determine os valores previstos para todos os dados valores.
Determine a diferença quadrada entre os valores y observados e a média dos valores y.
Determine a diferença quadrada entre os valores y previstos e a média dos valores y.
Determine a diferença quadrada entre os valores y observados e os valores y previstos.
Passo 2
Da tabela:
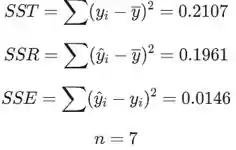
O coeficiente de determinação é a razão entre a soma dos quadrados da regressão SSR e a soma total dos quadrados SST:
Isso significa que 93.07% da proporção de variação observada na névoa pode ser atribuída à relação linear simples entre velocidade e névoa
Não há evidências substanciais de que o verdadeiro aumento médio em y seja inferior a 0.6, porque o aumento difere apenas de 0.6 por 0.01
Passo 3
O erro quadrático médio é a soma dos erros quadráticos dividido pelo tamanho da amostra diminuído por 2
O erro padrão da estimativa é a raiz quadrada do erro quadrado médio
O desvio padrão estimado de é o erro padrão dividido pelo desvio quadrado de x da média amostral.
Os graus de liberdade são o tamanho da amostra reduzido em 2:
O valor t crítico pode ser encontrado na tabela de distribuição T de Student no apêndice na linha de e na coluna de
Os limites do intervalo de confiança tornam-se então:
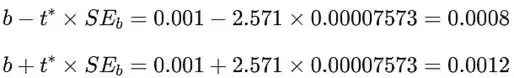
Resposta
- Sim
- 93.07%
- Não
- (0.0008,0.0012)