Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 3.2 - Ex. 30
De acordo com uma pesquisa, 55% dos habitantes de uma cidade se opõem a um cassino local. Desses 55%, cerca de 7 em cada 10 se opõem fortemente a um cassino. (Adaptado de: Rochester Business Journal.)
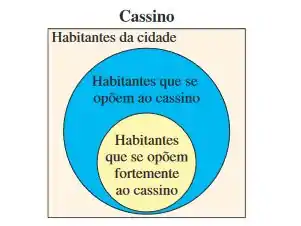
(a) Encontre a probabilidade de que um habitante selecionado aleatoriamente se oponha ao cassino e se oponha fortemente ao cassino.
(b) Encontre a probabilidade de que um habitante selecionado aleatoriamente que se opõe ao cassino não se oponha fortemente ao cassino.
(c) Seria incomum para um habitante selecionado aleatoriamente se opor ao cassino e se opor fortemente ao cassino? Explique.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A - A probabilidade é o número de resultados favoráveis dividido pelo número de resultados possíveis. Usando a regra da multiplicação, nós temos que
Sendo
Fazendo a substituição dos valores, nós temos que
Passo 2
B – Novamente, usando a regra da multiplicação, nós temos que
Substituindo os valores,
C – Não temos probabilidades incomuns para esses casos.