Acredita-se que o tempo (min.) para um assistente de laboratório preparar o equipamento para certo experimento tenha distribuição uniforme com e .
a. Escreva a fdp de e faça o gráfico.
b. Qual é a probabilidade de o tempo de preparação exceder 33 minutos?
c. Qual é a probabilidade de o tempo de preparação estar dentro de 2 minutos em relação à média? [Sugestão: leia no gráfico de .]
d. Para qualquer a tal que , qual é a probabilidade de o tempo de preparação estar entre a e min?
Passo 1
Falaaa, meu querido/minha querida. Como vai?? Nessa questão temos uma variável contínua, e para calcularmos as probabilidades vamos integrar a fdp no intervalo pedido. Bora láá!!!
Passo 2
O problema do enunciado tem distribuição uniforme entre e .
A função de densidade de probabilidade para distribuição uniforme é:
E o gráfico que representa ela é:
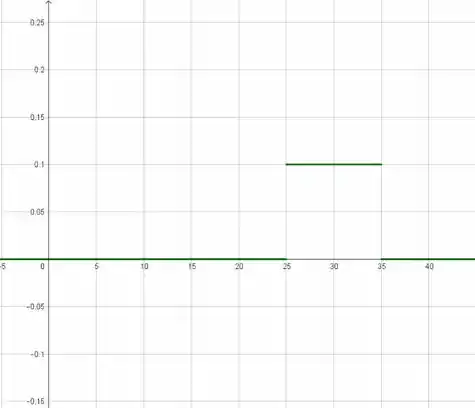
Passo 3
A probabilidade de uma variável contínua é a integral da fdp sobre o intervalo correspondente.
Passo 4
Primeiro calculamos a média que é a média dos limites:
Logo, 28 e 32 estão a dois minutos da média de 30.
E a probabilidade é definida por:
Passo 5
Por fim, a ultima probabilidade é calculada da seguinte forma:
Resposta
- .
- .
- .
- .