Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 4.Exercícios - Ex. 8

Para ir trabalhar, primeiro preciso tomar um ônibus perto da minha casa e depois mudar de ônibus. Se o tempo de espera (em minutos) em cada parada tem uma distribuição uniforme com A = 0 e B = 5 , pode ser mostrado que meu tempo total de espera Y tem a fdp

f y = 1 25 y                                                       0 ≤ y < 5 2 5 - 1 25 y                                   5 ≤ y ≤ 10 0                                           y < 0   o u   y > 10

a. Desenhe o gráfico da fdp de Y .

b. Demonstre que ∫ - ∞ ∞ f ( y )   d y = 1 .

c. Qual é a probabilidade de o tempo total de espera ser no máximo 3 min.?

d. Qual é a probabilidade de o tempo total de espera ser no máximo 8 min.?

e. Qual é a probabilidade de o tempo total de espera estar entre 3 e 8 min.?

f. Qual é a probabilidade de o tempo total de espera ser menos de 2 minutos ou mais de 6 minutos?

Passo 1

Falaaa, meu querido/minha querida. Como vai?? Nessa questão temos uma variável contínua, e para calcularmos as probabilidades vamos integrar a fdp no intervalo pedido. Bora láá!!!

Passo 2

O gráfico da fdp f ( y ) é descrito como:

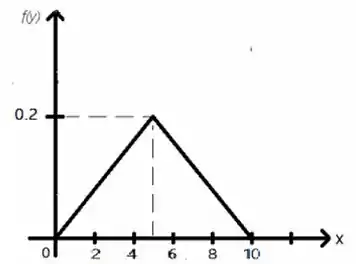
Passo 3

Para provarmos essa identidade, podemos usar a seguinte relação:

∫ - ∞ ∞ f ( y )   d y = á r e a   a b a i x o   d o   g r á f i c o

Como temos um triângulo com base 10 e altura 0,2. O seguinte é verdadeiro:

∫ - ∞ ∞ f ( y )   d y = 1 2 ∙ 0,2 ∙ 10 = 1

Passo 4

A probabilidade de que o tempo total de espera seja no máximo 3 minutos é dada por P ( Y ≤ 3 ) .

P Y ≤ 3 = ∫ 0 3 y 25 d y

= 1 25 3 2 2 - 0 2 2

P Y ≤ 3 = 0,18

Passo 5

A probabilidade de que o tempo total de espera seja no máximo 8 minutos é dada por P ( Y ≤ 8 ) .

P Y ≤ 8 = ∫ 0 5 y 25 d y + ∫ 5 8 2 5 - y 25 d y

= 1 25 5 2 2 - 0 2 2 + 2 5 8 - 5 - 1 25 8 2 2 - 5 2 2

P Y ≤ 8 = 0,92

Passo 6

Agora, para acharmos a probabilidade de o tempo de esperar for entre 3 e 8 minutos, podemos usar os resultados anteriores.

P 3 ≤ Y ≤ 8 = P Y ≤ 8 - P ( Y ≤ 3 )

= 0,92 - 0,18

P 3 ≤ Y ≤ 8 = 0,74

Passo 7

Por fim para acharmos a probabilidade se o tempo de espera ser menos que 2 minutos ou mais do que 6 minutos é escrita como:

P Y ≤ 2   o u   6 ≤ Y = P Y ≤ 2 + P ( 6 ≤ Y )

= ∫ 0 2 y 25 d y + ∫ 6 10 2 5 - y 25 d y

= 1 25 2 4 + 2 5 4 - 1 25 64 2

P Y ≤ 2   o u   6 ≤ Y = 0,4

Resposta

Resolução nos passos anteriores.

Exercícios de Livros Relacionados

De todos os clientes que compram portões automáticos de garagem, 75% compram um modelo acionado por corrente. Seja X = número entre os próximos 15 compradores que selecionam o modelo acionado por corr
98. Quando as placas de circuito usadas na fabricação de CD-players são testadas, a porcentagem de peças com defeito no longo prazo é 5%. Suponha que um lote de 250 placas tenha sido recebido e que a
95. O tempo de conclusão X de uma determinada tarefa possui fdc F(x) dada por 0 x0 x 3 3 0 ≤ x1 1 - 1 2 7 3 - x 7 4 - 3 4 x 1 ≤ x7 3 1 x ≥ 7 3 a. Obtenha a fdp f(x).b. Calcule P(0,5 ≤ X ≤ 2). c. Calcu
96. A tensão de ruptura de um determinado tipo de diodo escolhido aleatoriamente possui distribuição normal com valor de média 40 V e desvio padrão 1,5 V. a. Qual é a probabilidade de a voltagem de um
97. O artigo “Computer Assisted Net Weight Control” (Quality Progress, 1983, p. 22-25) sugere uma distribuição normal com média 137,2 onças e desvio padrão 1,6 onça para o conteúdo real de um tipo esp