Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 4.Exercícios - Ex. 6

O peso de tração real de um cartucho de som que está ajustado para rodas com 3g em um certo aparelho pode ser considerado uma va contínua X com fdp

f x = k [ 1 - x - 3 2 ]                               2 ≤ x ≤ 4 0                                                                 c a s o   c o n t r á r i o

a. Faça o gráfico de f ( x ) .

b. Determine o valor de k .

c. Qual é a probabilidade de o peso real de tração ser maior do que o nominal?

d. Qual é a probabilidade de o peso real estar dentro de 0,25g de distância em relação ao nominal?

e. Qual é a probabilidade de o peso real diferir do nominal em mais de 0,5g?

Passo 1

Falaaa, meu querido/minha querida. Como vai?? Para resolvermos essa questão, precisamos estar cientes que como f ( x ) é uma fdp, a condição a seguir deve ser satisfeita:

∫ - ∞ ∞ f ( x ) ∙ d x = 1

Sendo assim, bora fazer os cálculos que o enunciado pede!!!

Passo 2

O gráfico de f ( x ) pode ser analisado abaixo. As raízes da função permanecem a mesma, x = 2 e x = 4 , porém a altura irá variar conforme k varia.

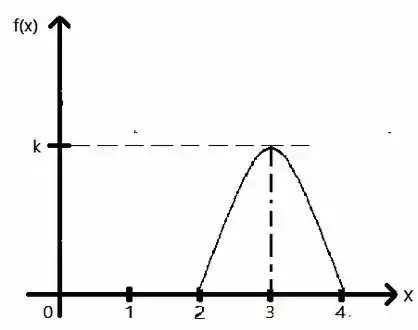
Passo 3

Para a dada fdp, temos:

∫ - ∞ ∞ f ( x ) d x = ∫ 2 4 k ( 1 - x - 3 2 ) d x = 1

k ∫ 2 4 ( 1 - x 2 + 6 x - 9 ) d x = 1

k ∙ 4 3 = 1

k = 3 4

Logo, a fdp pode ser escrita da seguinte forma:

f x = 3 4 1 - x - 3 2                       2 ≤ X ≤ 4 0                                                           c a s o   c o n t r á r i o

Passo 4

A probabilidade de que o peso real de rastreamento seja maior que o peso prescrito é P ( X > 3 ) , já que o peso é 3g.

P X > 3 = ∫ 3 4 3 4 1 - x - 3 2 d x

= 3 4 4 - 4 - 3 3 3 - 3 - 3 - 3 3 3

P X > 3 = 1 2

Passo 5

Agora, a probabilidade de que o peso real esteja dentro de 0,25g do peso prescrito é P ( 2,75 < X < 3,25 ) .

P 2,75 < X < 3,25 = ∫ 2,75 3,25 3 4 ( 1 - x - 3 2 ) d x

= 3 4 3,25 - 0,25 3 3 - 2,75 - 0,25 3 3

P 2,75 < X < 3,25 = 0,3672

Passo 6

Por fim, a probabilidade de que o peso real diferir em mais de 0,5 g do peso prescrito é P ( X < 2,5   o u   X > 3,5 ) , que pode ser rescrita como:

P X < 2,5   o u   X > 3,5 = 1 - P ( 2 , 5 ≤ X ≤ 3,5 )

Calculando a probabilidade.

P X > 3,5 = 1 - ∫ 2,5 3,5 3 4 1 - x - 3 2 d x

= 1 - 3 4 3,5 - 3,5 - 3 3 3 - 2,5 - 2,5 - 3 3 3

P X > 3,5 = 0,3125

Resposta

  1. Gráfico no passo 2.

  2. k = 3 / 4 .

  3. P X > 3 = 1 / 2 .

  4. P 2,75 < X < 3,25 = 0,3672 .

  5. P X > 3,5 = 0,3125 .

Exercícios de Livros Relacionados

93. Uma barra de 12 pol. fixa nas duas extremidades será submetida a uma tensão crescente até sua ruptura. Seja Y = distância da ruptura da barra em relação à extremidade esquerda. Suponha que Y tenha
A va binomial negativa X foi definida como o número de F’s antes do r-ésimo S. Seja Y = número de tentativas necessárias para obtenção do r-ésimo S. Da mesma forma que a fmp de X foi deduzida, deduza
Um amigo recentemente planejou uma viagem para um acampamento. Ele tinha duas lanternas, uma que exigia uma pilha de 6V e outra que usava duas pilhas tamanho D. Ele já havia colocado na mala duas pilh
Um sistema k-de-n funciona se, e somente se, pelo menos k dos n componentes individuais do sistema funcionarem. Se os componentes individuais funcionam independentemente um do outro, cada um com proba
Após embaralhar um baralho de 52 cartas, um crupiê dá cinco cartas. Seja X = número de naipes representados na mão de cinco cartas.Mostre que a fmp de X éCalcule μ ,σ 2 eσ