Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.3 - Ex. 6b
O acréscimo anual na área atingida por uma certa praga, numa região produtora
de frutas, pode ser modelado por uma variável aleatória contínua, medida em
hectares ( mil ) com densidade:
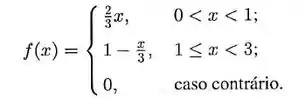
b. Qual seria a probabilidade da praga atingir entre e hectares esse ano?
Passo 1
Eai,tudo bem? Bora resolver mais um exercício?
O exercício nos pede para calcular a probabilidade da praga atingir entre e hectares esse ano.
Você se lembra desse conteúdo? Se não, é hora de dar aquela revisão. Ok?
Lembrando que esse gráfico é de uma função definida por partes.
Passo 2
Calculando a probabilidade da praga atingir entre e hectares esse ano, temos:
Resposta
Logo, a probabilidade da praga atingir entre e hectares esse ano é
Exercícios de Livros Relacionados
Suponha que o comprimento de fósseis encontrados em certa região, dado em centímetros, pode ser representado por uma variável aleatória X com função densidade de probabilidade dada por:A. Calcule a mé
Suponha que o comprimento de fósseis encontrados em certa região, dado em centímetros, pode ser representado por uma variável aleatória X com função densidade de probabilidade dada por:A. Calcule a mé
A largura do espaçamento é uma propriedade importante em um cabeçote magnético de gravação. Em unidades codificadas, se a largura for uma variável aleatória contínua ao longo da faixa de 0x2 , com f (
Determine a função de distribuição cumulativa para a distribuição no Exercício 4-1.
Determine a função de distribuição cumulativa para a distribuição no Exercício 4-6. Use a função de distribuição cumulativa para determinar a probabilidade de um componente resistir mais de 3000 horas