Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.3 - Ex. 5
Uma amostra de 20 observações de uma variável com distribuição Normal foi colhida, obtendo-se desvio padrão . No teste contra , foi estabelecido a região crítica Determine a probabilidade do erro tipo .
Passo 1
Temos então uma variável qualquer com distribuição normal.
O enunciado nos diz a variância amostral , mas não diz nada sobre a variância populacional ; portanto vamos ter de usar a seguinte aproximação:
Teremos o seguinte teste:
Passo 2
E foi dado pra gente também a região crítica:
Agora, lembrando que o erro tipo é a chance de rejeitarmos a hipótese nula sabendo que ela é verdadeira, ou seja, queremos a probabilidade de .
Então basta procurarmos na tabela de t-student um valor tal que:
Como RC é unilateral, na tabela vamos ter de procurar por uma coluna com e numa linha com 19 graus de liberdade:
Passo 3
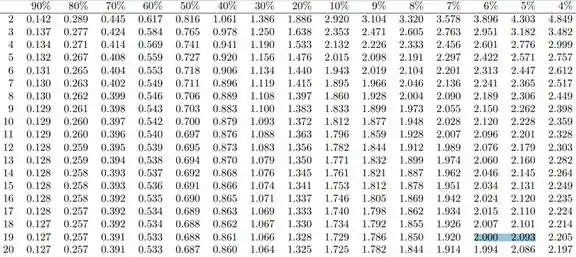
Teremos de usar interpolação, pois :
Se você lembrar, temos que fazer o seguinte:
Isolando chegamos em:
Esse representa o nosso dito anteriormente,ou seja, como Rc unilateral:
E essa é exatamente a chance de cometermo um erro tipo .
Resposta
Concluimos que a chance de rejeitarmos a hipótese nula e ela ser verdade, é de .