Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 2.5 - Ex. 39
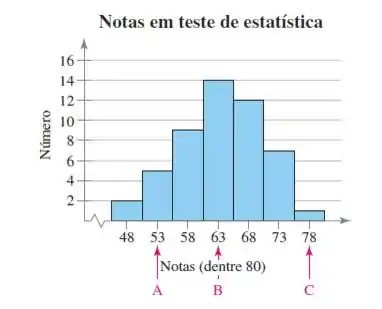
Análise gráfica. Os pontos médios A, B e C estão marcados no histograma. Relacione-os aos escores indicados. Qual escore, se existe algum, seria considerado incomum?
Passo 1
Oi galerinha, esse exercício é teórico, vem comigo que vou explicar direitinho para te ajudar!
Pelo histograma, conseguimos observar que o ponto médio é o ponto B, então o está relacionado com este ponto, pois é exatamente à média.
A partir deste ponto médio, podemos observar que o ponto A está abaixo da média, ou seja, é o escore relacionado, porque está 1,43 desvio padrão abaixo da média.
Sendo assim, o ponto C está relacionado com , ou seja, o ponto C está 2,14 desvio padrão acima da média.
Quando os valores da distribuição são padronizados, cerca de 95% dos escores devem estar entre -2 e 2, quando está fora desse intervalo é considerado incomum. Com isso, podemos considerar que o ponto C apresenta um escore incomum.
Espero que tenha conseguido te ajudar, até mais!
Resposta
- Ponto A ;
- Ponto B ;
- Ponto C ;
- Um escore de 2,14 seria incomum.