Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 21

O artigo “Effects of Bike Lanes on Driver and Bicyclist Behavior” (ASCE Transportation Eng. J., 1977, p. 243–256) relata os resultados de uma análise de regressão com x espaço percorrido disponível em pés (uma medida conveniente da largura da pista, definida como a distância entre um ciclista e a linha central da pista) e distância de separação y entre uma bicicleta e um carro em ultrapassagem (determinado por fotografia). Aqui seguem os dados para 10 ruas com pistas de ciclismo:

a. Demonstre que xi 154,20, yi 80, x2 i 2452,18, xi yi 1282,74 e y2 i 675,16. b. Deduza a equação da reta de regressão estimada. c. Que distância de separação você estimaria para outra pista com 15,0 de espaço disponível para trafegar? d. Qual seria a estimativa da distância de separação esperada de todas as ruas com um valor 15,0 de espaço percorrido utilizável?

Passo 1

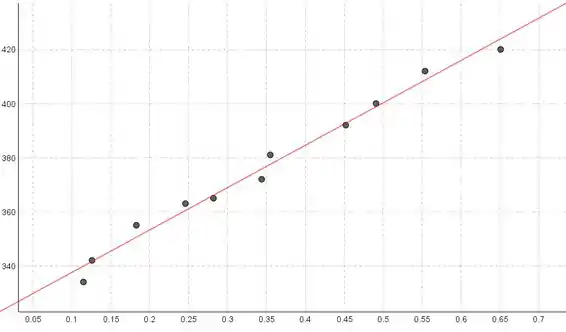  1. O gráfico de dispersão suporta o uso do modelo de regressão linear simples, porque o gráfico de dispersão não contém curvatura forte e o padrão parece ser aproximadamente linear.

    2. Além disso, na saída de regressão dada, notamos que R-quadrado é 98,5% e como esse valor é muito próximo de 100%, o modelo de regressão linear parece ser apropriado

    Passo 2

  2. Equação geral de regressão de mínimos quadrados:

    3. y ^ = β 0 + β 1 x

    A previsão do intercepto β 0 é o valor mencionado na linha com "constante" e na coluna de "Coef" da saída dada:

    b 0 = 321.878

    A previsão da inclinação β 1 é o valor mencionado na linha com "absorver" e na coluna de "Coef" da saída dada:

    b 1 = 156.711

    Substituir β 0 na equação de regressão dos mínimos quadrados por 3.2925 e substitua β 1 por 0.10748:

    y ^ = 321.878 + 156.711 x

    Substitua x na equação de regressão dos mínimos quadrados por 0.300:

    y ^ = 321.878 + 156.711 0.300 = 368.8913

    Assim, poderíamos prever um ângulo de resistência ao enrugamento de 368.8913 para uma amostra de tecido com uma absorbância de 0.300

    Passo 3

  3. Substitua x na equação de regressão dos mínimos quadrados por 0.300:

y ^ = 321.878 + 156.711 0.300 = 368.8913

Assim, a estimativa do ângulo de resistência ao enrugamento esperado é 368.8913, quando a absorbância é 0.300.

Resposta

  1. Sim
  2. 368.8919
  3. 368.8913

Exercícios de Livros Relacionados

Uma empresa quer estudar como varia o faturamento mensal Y , em milhões de cruzeiros, em função das quantidades vendidas de dois de seus produtos X 1 e X 2 . Para isso fez um levantamento mensal, dura
Num certo ano, foi feito um levantamento, em 10 estados brasileiros, a respeito do número de vagas oferecidas nas escolas de nível superior ( Y ), em 1.000 unidades, em função do número de candidatos
Num certo ano, foi feito um levantamento numa empresa, mês a mês, a respeito do custo total de fabricação por unidade produzida ( Y ), em cruzeiros, em função do gasto com matéria-prima ( X 1 ), em mi
Uma empresa quer estudar como varia o consumo de matéria-prima ( Y ), em toneladas, em função das quantidades produzidas de dois de seus produtos ( X 1 e X 2 ). Para isso fez um levantamento, mês a mê
Num certo ano, foi feito um levantamento numa empresa, mês a mês, a respeito do custo total de fabricação por unidade produzida ( Y ), em cruzeiros, em função do gasto com matéria-prima ( X 1 ), em mi