Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 23

Obtenha a SQE para os dados do Exercício 19 por meio da fórmula de definição [SQE (yi yˆi )2 ] e compare com o valor calculado por meio da fórmula de cálculo. b. Calcule o valor da soma dos quadrados total. O modelo de regressão linear simples parece ser eficaz para explicar uma variação na taxa de emissão? Justifique a sua afirmação

Passo 1

  1. A soma dos quadrados dos erros, SSE, é

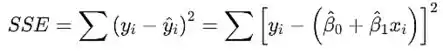
    2. A fórmula computacional para SSE é

    Primeiro estime a linha de regressão para calcular SSE sem fórmula computacional. Você faz isso por:

    A estimativa de mínimos quadrados da inclinação é

    b 1 = β ^ 1 = ∑ x i - x - y i - y - ∑ x i - x - 2 = S x y S x x

    S x y = ∑ x i y i - 1 n ∑ x i ∑ y i

    S x x = ∑ x i 2 - 1 n ∑ x i 2  

    A estimativa de mínimos quadrados da interceptação é

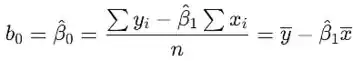
    A tabela a seguir com valores ajudará no cálculo dos valores correspondentes.

    O valor de S x y é

    S x y = ∑ x i y i - 1 n ∑ x i ∑ y i

    = 1413500 - 1 14 3300 ∙ 5010 = 3256000

    S x x = ∑ x i 2 - 1 n ∑ x i 2

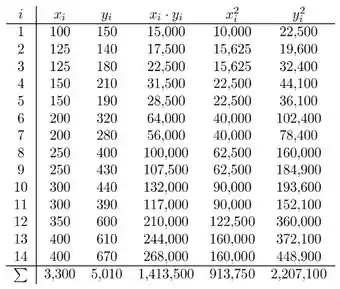
    = 913750 - 1 14 3300 2 = 1902500

    Passo 2

    Portanto, a estimativa da inclinação é

    b 1 = β ^ 1 = S x y S x x = 3256000 1902500 = 1.7114

    A estimativa da intercessão é

    b 0 =   β ^ 0 = ∑ y i - β ^ 1 ∑ x i n = 5010 - 1.7114 ∙ 3300 14 = - 45.5519

    A linha dos mínimos quadrados (a linha de regressão) torna-se

    y ^ = β ^ 0 + β ^ 1 x = - 45.5519 + 1.7114 x

    S S E = 150 - - 45.5519 + 1.7114 ∙ 100 2 + 140 - - 45.5519 + 1.7114 ∙ 125 2 + … + 670 - - 45.5519 + 1.7114 ∙ 400 2

    = 16213.64

    S S E = ∑ y i 2 - β 1 ^ ∑ x i y i

    = 2207100 - - 45.5519 5010 - 1.7114 ∙ 1413500

    = 16205.45

    Passo 3

  2. A soma total dos quadrados é

S S T = S y y = ∑ y i - y - 2 = ∑ y i 2 - 1 n ∑ y i 2

O coeficiente de determinação, r², é

r 2 = 1 - S S E S S T

Portanto, a soma total dos quadrados é

S S T = ∑ y i 2 - 1 n ∑ y i 2

= 2207100 - 1 14 5010 2 = 414236.71

O coeficiente de determinação é

r 2 = 1 - 16205.45 414235.71 = 0.961

O grande coeficiente de determinação indica que o modelo de regressão linear simples faz um trabalho eficaz de explicar a variação

Resposta

Ver o desenvolvimento.

Exercícios de Livros Relacionados

As rendas ( X ) e as vendas ( Y ), das 4 regiões do município de São Paulo, apresentaram, em 1971, as seguintes equações de regressão:Pede-se:Calcular e interpretar o coeficiente de correlação;Qual a
Uma empresa localizada na cidade de São Paulo, produtora de pneumáticos, possui uma rede distribuidora por todo o interior do Estado. Ela realizou um estudo para determinar qual a função que ligava o
Uma empresa fez um levantamento do custo total de um de seus produtos ( Y ), em mil cruzeiros, em função do número total de peças produzidas ( X ), em unidades, durante n = 5m e s e s , com a finalida
Uma empresa fez um levantamento do seu lucro mensal Y (em milhões de cruzeiros), em função das despesas gastas com propaganda X (em mil cruzeiros), durante n = 5m e s e s , com a finalidade de montar
Num certo ano, foi feito um levantamento, em 10 estados brasileiros, a respeito do número de vagas oferecidas nas escolas de nível superior ( Y ), em 1.000 unidades, em função do número de candidatos