Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 14.Exercícios propostos - Ex. 5
Uma empresa quer estudar como varia o faturamento mensal , em milhões de cruzeiros, em função das quantidades vendidas de dois de seus produtos e . Para isso fez um levantamento mensal, durante meses, e calculou:
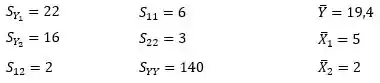
A partir desses valores, pede-se:
- Dar a equação da regressão linear múltipla que relaciona essas variáveis;
- Testar a existência dessa regressão, ao nível de significância de 5%, e calcular seu coeficiente de explicação.
Passo 1
Olá galerinha, tudo bem com vocês? Vem comigo!
No item a) queremos descobrir a equação da regressão linear múltipla. Para isso, precisamos encontrar os valores de , e , e faremos isso pelas seguintes equações:
Logo:
Por fim, temos a equação da regressão linear múltipla:
Passo 2
No item b) iremos testar a existência da regressão através da Análise de Variância representada pela tabela:
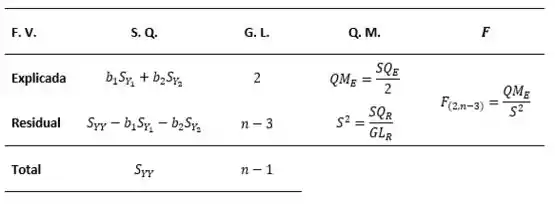
Se existe regressão de sobre e .
E o coeficiente de explicação é dada pela equação:
Primeiramente iremos encontrar nosso tabelado, onde:
- ;
- .
Para :
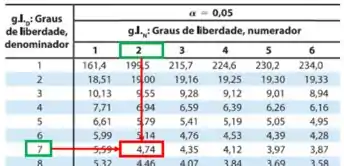
Passo 3
O cálculo das somas dos quadrados:
Completando nossa tabela de Análise de Variância:
Como (), então existe regressão de sobre e .
E por fim, iremos calcular o coeficiente de explicação:
Tchau galerinha. Até mais!
Resposta
- .
- Existe regressão ();
.