Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 5

O artigo "Objective Measurement of the Stretchability of Mozzarella Cheese" ( J . of Texture Studies, 1992, p. 185-194) descreveu um experimento realizado para investigar como o comportamento do queijo mussarela variou com a temperatura. Considere os dados a seguir sobre x = temperatura e y = elasticidade ( % ) na ruptura do queijo. (Observação: os pesquisadores eram italianos e usaram um queijo mussarela autêntico, não o "primo pobre" que pode ser obtido em quase qualquer parte dos Estados Unidos.)

a. Elabore um gráfico de dispersão em que os eixos se cruzam em ( 0,0 ) . Marque 0,20,40,60,80 e 100 no eixo horizontal e 0,50,100,150,200 e 250 no eixo vertical.

b. Elabore um gráfico de dispersão em que os eixos se cruzam em (55, 100), como foi feito no artigo citado. Será que esse gráfico parece preferível ao da parte (a)? Explique seu raciocínio.

c. O que os gráficos das partes (a) e (b) sugerem sobre a natureza da relação entre as duas variáveis?

Passo 1

E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:

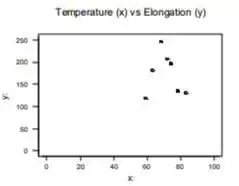
Elabore um gráfico de dispersão em que os eixos se cruzam em ( 0,0 ) . Marque 0,20,40,60,80 e 100 no eixo horizontal e 0,50,100,150,200 e 250 no eixo vertical.

a. O gráfico de dispersão com eixos que se cruzam em (0,0) é mostrado abaixo.

Passo 2

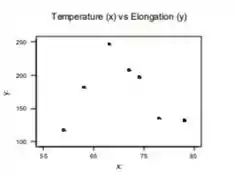
Elabore um gráfico de dispersão em que os eixos se cruzam em (55, 100), como foi feito no artigo citado. Será que esse gráfico parece preferível ao da parte (a)? Explique seu raciocínio.

b. O gráfico de dispersão com eixos que se cruzam em (55.100) é mostrado abaixo.

Passo 3

O que os gráficos das partes (a) e (b) sugerem sobre a natureza da relação entre as duas variáveis?

c. Uma parábola parece fornecer um bom ajuste para ambos os gráficos.

Resposta

a . O gráfico de dispersão com eixos que se cruzam em (0,0) é mostrado acima

b. O gráfico de dispersão com eixos que se cruzam em (55.100) é mostrado acima

c. Uma parábola parece fornecer um bom ajuste para ambos os gráficos.

Espero que tenham aprendido com essa questão, até a próxima !

Exercícios de Livros Relacionados

A probabilidade de um erro tipo II para o teste t de H0: 1 10 pode ser calculada da mesma maneira que para os testes t do Capítulo 8. Se o valor alternativo de 1 for representado por 1, o valor de é c
a. Verifique que E( ˆ 1) 1 usando as regras do valor esperado do Capítulo 5. b. Use as regras de variância do Capítulo 5 para verificar a expressão para V( ˆ 1) fornecida nesta seção.
Demonstre que, se cada xi for multiplicado por uma constante positiva c e cada yi for multiplicado por outra constante positiva d, a estatística t para testar H0: 1 0 versus Ha: 1 0 não muda em valor
Ao ajustar o modelo de regressão linear simples para as n = 27 observações sobre x = módulo de elasticidade e y resistência à flexão, no Exercício 15 da Seção 12.2, obtivemos yˆ 7,592, sˆ Y 0,179 quan
Realize o teste de utilidade do modelo, usando a abordagem ANOVA para os dados sobre taxa de filtragem–quantidade de umidade do Exemplo 12.6. Verifique se isso oferece um resultado equivalente ao do t