Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 43
A probabilidade de um erro tipo II para o teste t de H0: 1 10 pode ser calculada da mesma maneira que para os testes t do Capítulo 8. Se o valor alternativo de 1 for representado por 1, o valor de é calculado primeiro; depois, o conjunto de curvas apropriado na Tabela A.17 do apêndice será inserido no eixo horizontal, no valor de d, e o será reproduzido da curva para n 2 gl. Um artigo publicado no Journal of Public Health Engineering apresenta os resultados de uma análise de regressão baseada em n 15 observações, nas quais x temperatura de aplicação do filtro (°C) e y % eficiência da remoção de DBO. As quantidades calculadas incluem xi 402, x2 i 11.098, s 3,725 e ˆ 1 1,7035. Experimente testar, no nível 0,01, H0: 1 1, que expressa que o aumento esperado na % de remoção de DBO é 1, quando a temperatura de aplicação do filtro aumenta 1°C, comparando-a com a alternativa Ha: 1 1. Determine P(erro tipo II) quando 1 2, 4
Passo 1
A probabilidade de um erro tipo II para o teste t quando testamos hipóteses:
precisamos calcular o valor:
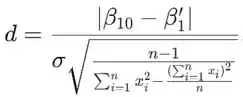
Para obter a probabilidade tipo II usamos a tabela A.17 do Apêndice onde o valor d está no eixo x e está no eixo y. Usamos probabilidade para curva que tem graus de liberdade.
Nesta tarefa temos as seguintes informações
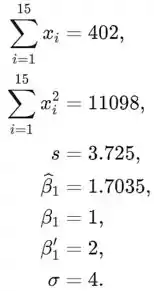
Passo 2
Agora vamos testar as hipóteses . Temos a seguir
Sabemos que o grau de liberdade para a estatística t é e o valor de d calculamos e obtivemos que é 1.2. Agora podemos considerar os gráficos apresentados acima. Se usarmos que a probabilidade do tipo I é 0.05 a probabilidade do tipo II será quase zero. Mas se usarmos que a probabilidade do tipo I é 0.01 obtemos que a probabilidade do tipo II é quase 0.1.
Resposta
Calculamos a probabilidade do tipo II e será quase 0.1 no caso de probabilidade do tipo I igual a 0.01