O artigo "Origin of Precambrian Iron Formations" (Econ. Geology, 1964, p. 1025-1057) relata os seguintes dados sobre o total de Fe de quatro tipos de formação de ferro (I carbonato, 2 silicato, 3 magnetita, 4 hematita).
Implemente uma análise do teste F de variância no nível de significância 0,01 e apresente o resumo dos resultados em uma tabela ANOVA
Passo 1
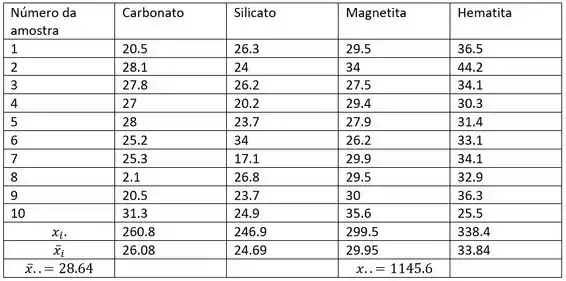
esta tabela resume tudo o que é necessário para realizar o teste F. Aqui está a explicação de como obter esses valores.
Passo 2
Observe primeiro que
E
A tabela a seguir precisa ser preenchida com os valores correspondentes:
 Os graus de liberdade são
Os graus de liberdade são
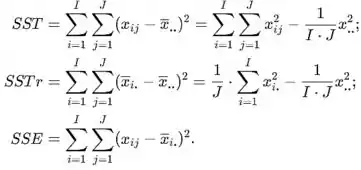
Os quadrados médios são
F é a razão dos dois quadrados médios
Calcule todos os valores um por um. Ao somar as colunas correspondentes (geralmente linhas), valores de são
Passo 3
Valores
São dados por
A grande média é
E
A soma total dos quadrados é
A soma dos quadrados do tratamento é
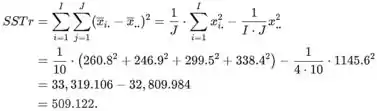
A identidade fundamental diz:
A soma dos quadrados do erro é
Os quadrados médios podem ser calculados agora como
O valor estatístico F é
A tabela ANOVA agora se torna

Quanto aos testes usuais, você pode tirar conclusões sobre as hipóteses observando o valor crítico de F ou um valor de P. Lembre-se que as hipóteses de interesse são
versus hipótese alternativa
O valor P é a área à direita do valor f sob a curva F onde F tem distribuição de Fisher com graus de liberdade 3 e 36; portanto
que foi calculado usando software (você pode estimá-lo usando a tabela no apêndice). Porque
Rejeitamos a hipótese nula em determinado nível de significância. Não há diferença estatisticamente significativa nas médias verdadeiras entre os quatro tipos de formação de ferro.
Usando a tabela, você pode usar, por exemplo, valor para o qual a área sob a curva F à direita de é 0,1. O valor é
o que indica rejeitar a hipótese nula.
Resposta
Rejeitar a hipótese nula em qualquer nível de significância razoável