Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 10.Exercícios - Ex. 9
Foram analisadas seis amostras de cada um dos quatro tipos de grão de cereal cultivados em uma região para determinar o teor de tiamina, o que gerou os seguintes dados (µg/g):
Será que esses dados sugerem que pelo menos dois tipos de grão são diferentes em relação ao teor médio real de tiamina? Use um nível de teste com base no método do valor P
Passo 1
Note que primeiro temos
E
A tabela a seguir precisa ser preenchida com os valores correspondentes:
Os graus de liberdade são
Temos que
A soma total dos quadrados (SST), tratamento soma de quadrados (SSTr), e erro soma dos quadrados (SSE) são dados por
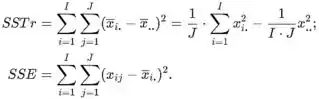
Passo 2
Os quadrados médios são
F é a razão dos dois quadrados médios
Calcule todos os valores um por um. Ao somar as colunas correspondentes (geralmente linhas), valores de são
Passo 3
Valores de são dados por
A grande média é
E
A soma total dos quadrados é
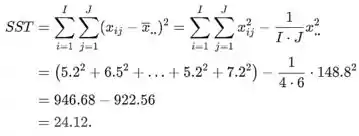
A soma dos quadrados do tratamento é
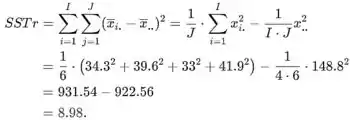
A identidade fundamental
A soma dos quadrados do erro é
Os quadrados médios podem ser calculados agora como
O valor da estatística F é
A tabela ANOVA agora se torna
Quanto aos testes usuais, você pode tirar conclusões sobre as hipóteses observando o valor crítico de F ou um valor de P. Lembre-se que as hipóteses de interesse são
Versus a hipótese alternativa
O valor P é a área à direita do valor f sob a curva F onde F tem distribuição de Fisher com graus de liberdade 3 e 20; portanto
que foi calculado usando software (você pode estimá-lo usando a tabela no apêndice). Porque
rejeitar hipótese nula em determinado nível de significância.
Usando a tabela, você pode usar, por exemplo, valor para o qual a área sob a curva FF à direita de é 0.05. O valor é
E o valor para o qual a área sob a curva F à direita de é
assim, vale o seguinte
então o valor de P está entre 0.01 e 0.05 o que indica a rejeição da hipótese nula no nível de significância 0.05.
Resposta
Rejeitar a hipótese nula.