Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 10.Exercícios - Ex. 7
Em um experimento para investigar o desempenho de quatro marcas diferentes de velas de ignição que seriam usadas em motos de 125 cc de dois tempos, cinco velas de cada marca foram testadas, observando-se o número de milhas percorridas (com velocidade constante) até o momento em que apresentassem falha. Uma tabela de dados ANOVA parcial é apresentada aqui. Preencha os campos vazios, expresse as hipóteses relevantes e faça um teste, obtendo o máximo possível de informações sobre
Passo 1
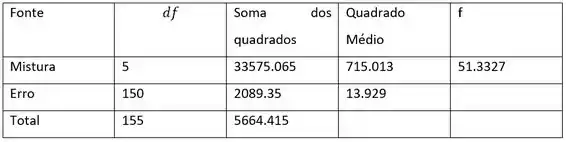
Dado:
Assumindo que:
A hipótese nula afirma que todas as médias populacionais são iguais:
A hipótese alternativa afirma o oposto da hipótese nula:
Os graus de liberdade do tratamento são o número de grupos diminuído em 1:
Os graus de liberdade para o erro é o tamanho total da amostra diminuído pelo número de grupos
O total de graus de liberdade é a soma dos dois graus de liberdade anteriores:
Passo 2
A soma dos quadrados dos erros é o produto do erro quadrático médio e os graus de liberdade para o erro:
A soma dos quadrados do tratamento é a soma dos quadrados total diminuída pela soma dos quadrados do erro:
O quadrado médio do tratamento é a soma dos quadrados do tratamento dividida pelos graus de liberdade para o tratamento:
A estatística ANOVA F é a razão entre o MSTr e o MSE:
Passo 3
O valor P é a probabilidade de obter o valor da estatística de teste, ou um valor mais extremo. O valor P é o número (ou intervalo) no título da coluna da Tabela 8 contendo o valor F na linha e :
Se o valor P for menor que o nível de significância, rejeite a hipótese nula.
Há evidências suficientes para apoiar a afirmação de que as médias populacionais não são todas iguais.
Resposta
Há evidências suficientes para apoiar a afirmação de que as médias populacionais não são todas iguais.