Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios - Ex. 40
O artigo “Readability of Liquid Crystal Displays: A Response Surface” (Human Factors, 1983, p. 185–190) usou um modelo de regressão múltipla com quatro variáveis independentes para investigar a precisão de leitura em monitores ou telas de cristal líquido (LCDs). As variáveis eram
a. Calcule uma estimativa da porcentagem de erros esperada quando x1 10, x2 0,5, x3 50 e x4 100. b. Estime a porcentagem média de erros em relação a um nível 20 para a lâmpada traseira, 0,5 para a subtensa do caractere, 10 para o ângulo de visão e 30 para o nível de luz ambiente. c. Qual é a mudança esperada estimada na porcentagem de erros quando o nível de luz ambiente sofre um aumento de 1 unidade e todas as outras variáveis são fixadas nos valores fornecidos na parte (a)? Responda para um aumento de 100 unidades no nível de luz ambiente. d. Explique por que as respostas na parte (c) não dependem dos valores fixos de x1, x2 e x3. Sob que circunstâncias haveria essa dependência? e. O modelo estimado baseou-se em n 30 observações, com SQT = 39,2 e SQE = 20,0. Calcule e interprete o coeficiente de determinação múltipla e, em seguida, realize o teste de utilidade do modelo usando 0,05.
Passo 1
- Nesta subseção, precisamos calcular a porcentagem de erro esperado do valor previsto onde
- Nesta subseção, precisamos calcular a porcentagem de erro esperado do valor previsto onde
- Deixe a variável ter os mesmos valores que na subseção (a) e a variável é crescente para 1 unidade. Significa que o novo valor para a variável é
- A mudança esperada estimada na porcentagem de erro não depende dos valores fixos porque essas variáveis são independentes com a variável . E quando a variável aumentando ou diminuindo apenas as mudanças que temos perto dessa variável. Não influencia no resto da equação.
- Temos que este modelo de previsão está usando 30 observações onde a soma total dos quadrados é 39.2 e a soma total dos erros é 20. Agora precisamos encontrar R² e então precisamos usar teste de utilidade para testar hipóteses sobre coeficientes com nível de confiança 0.95. Temos o seguinte:
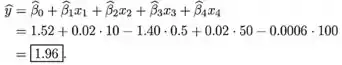
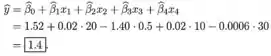
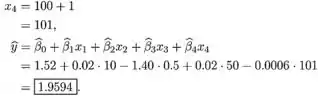
O valor esperado diminuirá para .
Quando a variável aumentar para 1 unidade, a porcentagem de erro esperada prevista diminuirá para 0.0006. Por causa disso, se a variável aumentar para 100 unidades, a porcentagem de erro prevista diminuirá para 0.0006⋅100=0.006.
Passo 2
As hipóteses de teste são calculadas da seguinte forma:
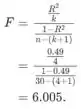
Esta estatística tem distribuição e o valor crítico é dado abaixo:
Como a estatística F tem valor maior que o valor crítico significa que rejeitamos hipóteses nulas e aceitamos alternativas, e.c. este modelo é bom porque pelo menos um coeficiente é diferente de zero.
Resposta
Ver o desenvolvimento.