Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios Suplementares - Ex. 70
O resultado do SAS apresentado a seguir baseia-se em dados extraídos do artigo “Evidence for and the Rate of Denitrification in the Arabian Sea” (Deep Sea Research, 1978, p. 431–435). As variáveis em estudo são x nível de salinidade (%) e y nível de nitrato ( M/L). a. Qual é o tamanho da amostra n? [Sugestão: procure graus de liberdade para SQE.] b. Calcule uma estimativa pontual do nível de nitrato esperado quando o nível de salinidade é 35,5. c. Parece haver alguma relação linear útil entre as duas variáveis? d. Qual é o valor do coeficiente de correlação amostral? e. Você usaria o modelo de regressão linear simples para tirar conclusões quando o nível de salinidade fosse 40?
Passo 1
A estimativa de mínimos quadrados da inclinação no modelo de regressão linear simples é
Onde é
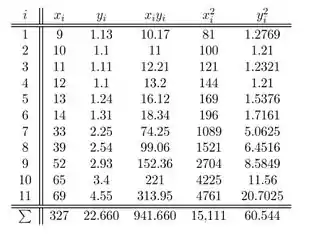
Encontrando e usando a soma dada no exercício, a estimativa para a intersecção é
A equação de regressão linear é então
Passo 2
Para calcular o intervalo de previsão quando , calcule SE que é dado no exercício.
A estimativa do desvio padrão σ é
A soma dos quadrados dos erros, SSE, é
A fórmula computacional para SSE é
Passo 3
Calibrar valor de quando
Finalmente, por exemplo, um intervalo de previsão de 95% é
Pode ser que o indivíduo mencionado tenha menos de 22 anos porque 22 pertences ao intervalo acima