Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 8.Exercícios - Ex. 35
8-35.Um artigo na revista Computers&Electrical Engineering."Parallei simularion of cellular neural network"-Simulacao paralela de redesneurais celulares(1996,Vol.22.pp.61 84)considerou a aceleragao de redes neurais celulares(RNC)para uma arquitetura computacional paralela com finalidade geral.baseada em seis transputers cm diferentes areas.Os dados sao mostrados a seguir:
（a)Ha evidencia para suportar a suposicao de que a aceleracao de RNC normalmente distribuida?Inclua um grafico cm sua resposta.
（b)C'onstrua um intervalo bilateral de confianga de 959 para a aceleracao media.
（c)Construa um limite inferior de confianca de 95% para a aceleracao media.
Passo 1
Vamos lá pessoal, se liga aqui como que resolve essa questão:
Letra a:
Crie um gráfico de probabilidade normal.
Os valores dos dados estão no eixo horizontal e as pontuações normais padronizadas estão no eixo vertical.
Se os dados contiverem n valores de dados, então as pontuações normais padronizadas são os valores z na tabela III correspondendo a uma área de (ou a área mais próxima) com ;
A menor pontuação padronizada corresponde ao menor valor de dados, a segunda menor pontuação padronizada corresponde ao segundo menor valor de dados e assim por diante.
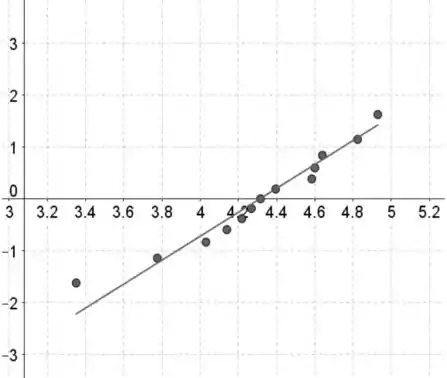
O gráfico de probabilidade normal não contém curvatura forte e o padrão é aproximadamente linear, então podemos concluir que os valores dos dados são aproximadamente normalmente distribuídos.
Passo 2
Letra b
A média é a soma de todos os valores dividida pelo número de valores:
n é o número de valores no conjunto de dados.
A variação é a soma dos desvios de quadráticos da média dividida por n - 1. O desvio padrão é a raiz quadrada da variância:
Determine o valor de t olhando na linha começando com graus de liberdade e na coluna com na tabela V:
O intervalo de confiança é:
Preenchendo os valores conhecidos:
Simplificando:
Passo 3
Letra c:
A média é a soma de todos os valores dividida pelo número de valores:
n é o número de valores no conjunto de dados.
A variação é a soma dos desvios de quadráticos da média dividida por n - 1. O desvio padrão é a raiz quadrada da variância:
Determine o valor de t olhando na linha começando com graus de liberdade e na coluna com na tabela V:
O intervalo de confiança inferior é:
Preenchendo os valores conhecidos:
Simplificando:
Resposta
- Aproximadamente distribuído normalmente