Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 46
O artigo “The Incorporation of Uranium and Silver by Hydrothermally Synthesized Galena” (Econ. Geology, 1964, p. 1003–1024) descreve a determinação do volume de prata nos cristais de galena formados em um sistema hidrotérmico acima de uma amplitude de temperatura. Sendo x temperatura de cristalização em °C e y Ag2S em %mol, os dados são:
de onde xi 6130, x 2 i 3.022.050, yi 4,73, y 2 i 2,1785, xi yi 2418,74, ˆ 1 0,00143, ˆ 0 0,311, e s 0,131. a. Estime o volume médio real de prata quando a temperatura é de 500°C usando um intervalo de confiança de 95%. b. Como a amplitude de um IC de 95% para o volume médio real de prata (quando a temperatura é de 400°C) pode se comparar com a amplitude do intervalo na parte (a)? Responda sem calcular esse novo intervalo. c. Calcule um IC de 95% para uma mudança média real no volume de prata associada com um aumento de temperatura de 1°C. d. Suponha que se tenha acreditado antes que, quando a temperatura de cristalização fosse de 400°C, o volume médio real de prata seria de 0,25. Realize um teste ao nível de significância 0,05 para verificar se os dados amostrais contradizem esse ponto de vista prévio.
Passo 1
- O valor previsto é obtido avaliando a linha de regressão estimada em
- O valor 0 está mais longe da média amostral que o valor .
- Determine o valor t olhando na linha começando com graus de liberdade e na coluna com (bicaudal) na tabela da distribuição T de Student:
- O valor previsto é obtido avaliando a linha de regressão estimada em
A média amostral é a soma de todos os valores dividido pelo número de valores:
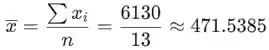
Determine o valor t olhando na linha começando com graus de liberdade e na coluna com (bicaudal) na tabela da distribuição T de Student
Determine a margem de erro:
Os limites do intervalo de confiança tornam-se então:
Estamos 95% confiantes de que o verdadeiro teor médio de prata quando a temperatura é de 500°C está entre 0.3209 mol% e 0.4871 mol%
Passo 2
Quanto mais distante o valor x estiver da média dos valores x, menos precisas serão as previsões e, portanto, mais amplo será o intervalo de confiança.
Isso então implica que o intervalo de confiança de 95% quando a temperatura é 400°C é maior que a largura do intervalo de confiança de 95% na parte (a).
O desvio padrão da inclinação é o desvio padrão s do desvio aleatório dividido pela raiz quadrada de
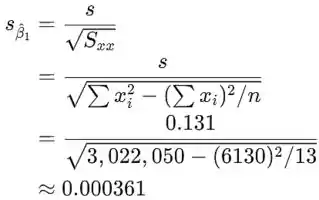
Os limites do intervalo de confiança para são então:
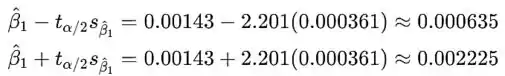
Estamos 95% confiantes de que a verdadeira mudança média no teor de prata associada a um aumento de 1°C na temperatura está entre 0,000635 mol% e 0.002225 mol%.
Passo 3
A média amostral é a soma de todos os valores dividido pelo número de valores:
Determine o valor t olhando na linha começando com graus de e na coluna com (bicaudal) na tabela da distribuição T de Student:
A margem de erro é:
Os limites do intervalo de confiança tornam-se então:
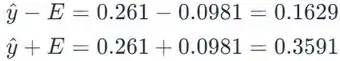
Estamos 95% confiantes de que o verdadeiro teor médio de prata quando a temperatura é de 500°C está entre 0,1629 mol% e 0,3591 mol%.
Como 0,25 está entre 0,1629 e 0,3591, é plausível que o verdadeiro teor médio de prata seja 0,25 e, portanto, concluímos que não há evidências suficientes para apoiar a afirmação de que os dados da amostra contradizem essa crença anterior
Resposta
- Mais Largo
- Não há evidências suficientes para apoiar a afirmação de que os dados da amostra contradizem essa crença anterior.