Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 12.Exercícios - Ex. 45
Reconsidere os dados sobre taxa de filtragem–quantidade de umidade introduzidos no Exemplo 12.6 (veja também o Exemplo 12.7). a. Calcule um IC de 90% para 0 1251, a quantidade média real de umidade quando a taxa de filtragem é 125. b. Preveja o valor da quantidade de umidade para uma única operação experimental na qual a taxa de filtragem é 125 usando um nível de previsão de 90%. Como esse intervalo se compara ao intervalo da parte (a)? Por que isso ocorre? c. Em que os intervalos das partes (a) e (b) se comparam com o IC e o IP quando a taxa de filtragem é 115? Responda sem de fato calcular esses novos intervalos. d. Interprete as hipóteses H0: 0 1251 80 e H0: 0 1251 80, e, em seguida, realize um teste ao nível de significância 0,01.
Passo 1
-
Seja ser um valor fixo de x. Para a variável aleatória
vale o seguinte:
A variância da variável aleatória é
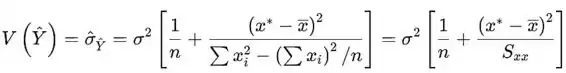
O desvio padrão é a raiz quadrada da expressão. Ao substituir (estimar) \ por s você obtém a estimativa da variância e/ou desvio padrão da variável aleatória .
Um intervalo de confiança de para a média de Y quando é
Um intervalo de confiança de 90% para a média de Y quando é necessário. Primeiro calcule
onde os valores marcados em azul são dados nos exemplos mencionados.
Da tabela no apêndice, para e graus de liberdade 2=18 o t valor é
A estimativa do desvio padrão da variável aleatória é
onde os valores marcados em azul foram retirados dos exemplos mencionados.
Finalmente, um intervalo de confiança de 90% para a média de Y quando é
Passo 2
- Intervalo de previsão
é um intervalo de previsão de para uma observação futura Y, quando
Os valores necessários para calcular um intervalo de previsão de 90% podem ser encontrados em (a); assim, um intervalo de previsão de 90% quando é
O intervalo de previsão é mais largo que o intervalo de confiança calculado em (a). Isso ocorre porque o erro padrão é maior para o intervalo de previsão.
Sem calcular o CI e o PI, observe que o valor
o que implica que
portanto, o erro padrão do IC e do PI quando x=115 será maior e o IC e o PI serão mais largos do que o IC e o PI quando x=125.
Passo 3
A interpretação das hipóteses seria testar, quando a taxa de filtração fosse de 125 kg DS/m/h, se a umidade média é igual ou inferior a 80%.
Ao testar contra uma das alternativas, o valor da estatística de teste é
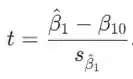
Dependendo da hipótese alternativa, o valor P pode ser determinado como área correspondente sob . O teste de utilidade do modelo
Os valores requeridos podem ser encontrados na solução (em (a)(a)); assim, o valor da estatística de teste é
O valor de P, por causa da hipótese alternativa, é
onde o valor foi calculado por software e a variável aleatória T tem distribuição de Student com graus de liberdade n-2=20-2=18. Porque
rejeitar a hipótese nula em determinado nível de significância. É estatisticamente significativo que a umidade média seja inferior a 80% quando a taxa de filtração for 125.
Resposta
- (77.797,78.378);
- (76,895, 79,281);
- CI e PI mais amplos quando x=115;
- Rejeitar a hipótese nula