O artigo “The Luminosity–Spectral Index Relationship for Radio Galaxies” (Nature, 1972, p. 88–89) propôs que, para as galáxias da classe S, ln(L178) está relacionada linearmente com o índice espectral, onde L178 representa luminosidade a 178 MHz. Aqui são apresentados os dados representativos:
a. Estime os parâmetros do modelo exponencial sugeridos pela relação linear entre ln(L178) e o índice espectral. b. Que valor de L178 seria previsto para um índice espectral de 0,75? c. Calcule um intervalo de previsão de 95% para a luminosidade quando o índice espectral é 0,95
Passo 1
O gráfico de dispersão de y versus x não mostra nenhum padrão específico. uma regressão linear não é apropriada. No entanto, o gráfico de dispersão de versus x sugere que talvez um modelo linear seja apropriado de certa forma.
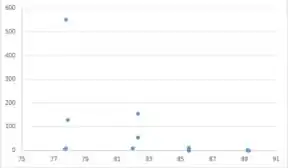
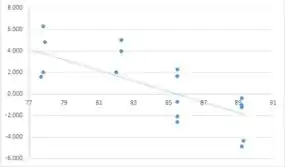
É necessário ajustar um modelo de regressão linear simples aos dados transformados (usando , no entanto, com um leve abuso de notação a
na verdade, representará para facilitar o entendimento) para fazer uma previsão válida e calcular um intervalo de previsão para .
A estimativa de mínimos quadrados da inclinação no modelo de regressão linear simples é
![]()
![]()
![]()
A estimativa de mínimos quadrados da interceptação é
![]()
Passo 2
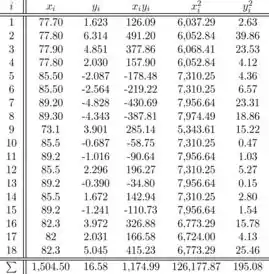
As seguintes somas são necessárias para calcular as estimativas de mínimos quadrados, e são dadas no exercício (estes valores são arredondados):
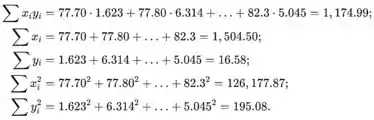
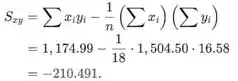
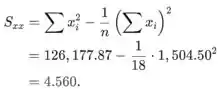
![]()
Encontrando usando as somas dadas acima, a estimativa do intercepto é
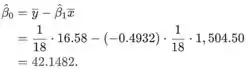
Um intervalo de previsão de 95% para quando deve ser calculado.
Intervalo de previsão
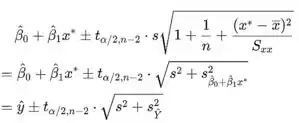
é um intervalo de previsão de para uma observação futura Y, quando .
O valor de quando , usando o modelo de regressão linear simples, é
![]()
A variância de uma variável aleatória é
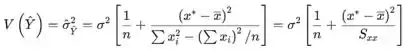
O desvio padrão é a raiz quadrada da expressão. Ao substituir (estimar) σ por s você obtém a estimativa da variância e/ou desvio padrão da variável aleatória
Passo 3
A soma dos quadrados dos erros, SSE, é
![]()
A estimativa do desvio padrão σ é
![]()
A soma dos quadrados dos erros, SSE, é
![]()
A fórmula computacional para SSE é
![]()
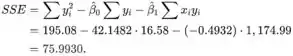
A estimativa do desvio padrão de é

Os valores necessários para calcular um intervalo de previsão de 95% podem ser encontrados acima; assim, um intervalo de previsão de 95% quando é

Este é um intervalo de previsão de quando . Tomando o antilog um intervalo de previsão de 95% para o valor original de y quando é
![]()
Há muitas outras maneiras de ver a validade do ajuste; no entanto, eles não serão apresentados aqui.
Resposta
Não é bom ajuste; (0.1194,1811.9333)