Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios - Ex. 15
Nenhum aficionado por chips de tortilla gosta de chips engordurados, de modo que é fundamental identificar características do processo de produção que resultem chips com uma textura atraente. Os dados a seguir sobre x tempo de fritura (s) e y quantidade de umidade (%) foram apresentados no artigo “Thermal and Physical Properties of Tortilla Chips as a Function of Frying Time” (J. of Food Processing and Preservation, 1995, p. 175–189).
a. Construa um gráfico de dispersão de y versus x e comente. b. Construa um gráfico de dispersão de pares (ln(x), ln(y)) e comente. c. Que relação probabilística entre x e y é sugerida pelo padrão linear no gráfico do item (b)? d. Presuma o valor da quantidade de umidade quando o tempo de fritura é 20, de uma maneira que transmita informações sobre confiabilidade e precisão. e. Analise os resíduos do ajuste do modelo de regressão linear simples aos dados transformados e comente
Passo 1
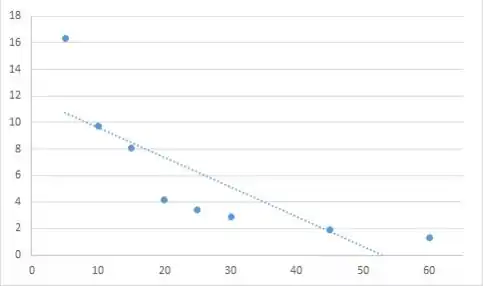
- O gráfico de dispersão sugere que há um padrão curvo; assim, um modelo de regressão linear simples não é apropriado
-
Calcule o logaritmo natural de . A tabela a seguir contém valores de logaritmos naturais
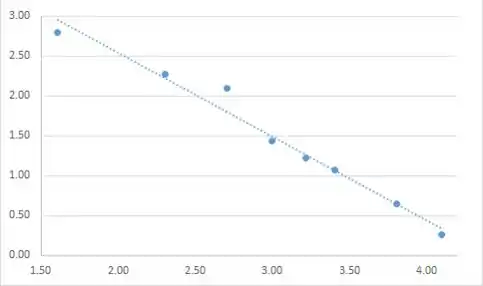
O gráfico de dispersão sugere uma relação linear entre as variáveis; isso, um modelo de regressão linear é apropriado.
- O modelo probabilístico apropriado seria
- É necessário ajustar um modelo de regressão linear simples aos dados transformados para fazer uma previsão válida e calcular um intervalo de previsão para . A estimativa de mínimos quadrados da inclinação no modelo de regressão linear simples é
- O valor ajustado são valores obtidos substituindo na linha de regressão. Os resíduos são a diferença entre os valores observados e ajustados.
que é uma função de potência. Isso ocorre porque o uso do logaritmo natural de ambas as variáveis produz um forte padrão linear
Passo 2
A estimativa de mínimos quadrados da interceptação é
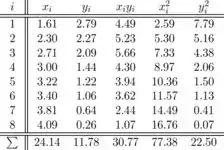
As seguintes somas são necessárias para calcular as estimativas de mínimos quadrados, e são dadas no exercício (estes valores são arredondados):
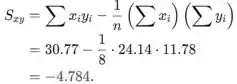
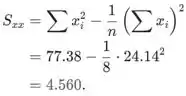
Usando os resultados anteriores, temos que
Encontrando e usando as somas dadas acima, a estimativa do intercepto é
é um intervalo de previsão de para uma observação futura Y, quando .
O valor de quando , usando o modelo de regressão linear simples, é
A variância de uma variável aleatória é
O desvio padrão é a raiz quadrada da expressão. Ao substituir (estimar) σ por s você obtém a estimativa da variância e/ou desvio padrão da variável aleatória .
A soma dos quadrados dos erros, SSE, é
O desvio padrão estimado é
A soma dos quadrados dos erros, SSE, é
A fórmula computacional para SSE é
Pela fórmula computacional, o valor de SSE é
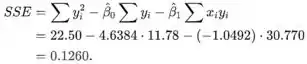
Portanto, a estimativa de σ é
A estimativa do desvio padrão de é
Os valores necessários para calcular um intervalo de previsão de 95% podem ser encontrados acima; assim, um intervalo de previsão de 95% quando é
Este é um intervalo de previsão para . Tomando o antilog um intervalo de previsão de 95% para o valor original de y quando é
Passo 3
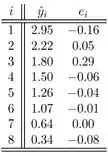
Os valores ajustados foram calculados usando a linha de regressão linear simples estimada acima da seguinte forma
também, os resíduos são
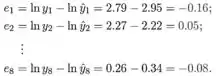
A relação de resíduos versus valores ajustados mostra que existe um outlier, um resíduo muito grande. Existem dois resíduos positivos enquanto todos os outros são negativos, próximos de zero.
O gráfico de probabilidade normal dos resíduos sugere normalidade. Pode-se analisar também os resíduos padronizados, mas não é necessário.
Gráfico Residual
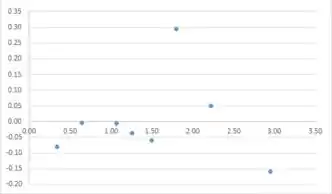
Gráfico de probabilidade normal
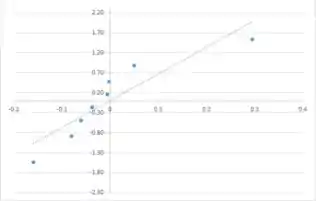
Resposta
Ver o desenvolvimento