Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.3 - Ex. 1c
Com o auxílio da tabela calcule:
(c)
Passo 1
Novamente, lembrando que a tabela nos fornece valores de , para os quais:
Para a letra C, vamos buscar o seguinte:
Então, teremos duas probabilidades unilaterais, quando isso acontece(Probabilidades unilaterais) em vez de:
Teremos:
Então, vamos buscar na tabela, dois valores , e vamos analisar a coluna em que estão:
Passo 2
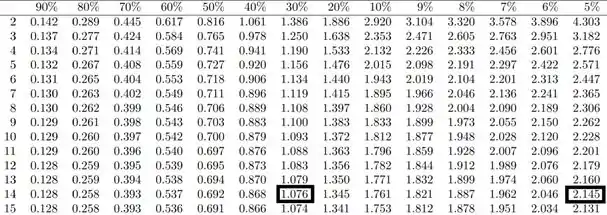
Vamos aproximar porque não somos obrigados, né?!
Perceba que:
E
Só que:
Então:
E
Passo 3
OBs: Muita atenção aos sinais:
E
Lembra da regrinha do “E”, se queremos , então basta multiplicar essas probabilidades:
Tranquilo né?
Resposta
(c)
Exercícios de Livros Relacionados
Uma amostra de 20 observações de uma variável com distribuição Normal foi colhida, obtendo-se desvio padrão 1,1 . No teste μ = 5 contra μ5 , foi estabelecido a região crítica t ∈ R t2,033 } . Determin
O número de pontos de um exame de inglês tem sido historicamente ao redor de 80. Sorteamos 10 estudantes que fizeram o exame recentemente e observamos as notas: 65 ; 74 ; 78 ; 86 ; 59 ; 84 ; 75 ; 72 ;
O crecimento de bebês, durante o primeiro mês de vida, pode ser modelado pela distribuição normal. Admite que, em média, um crescimento de 5 centímetros ou mais seja considerado satisfatório. Deseja-s
Testes exaustivos realizados pela indústria Cookbem indicam que seu forno de micro-ondas tem probabilidade0,1 de apresentar a 1 a. falha antes de 900 horas de uso. Um novo método de produção está send
Testes exaustivos realizados pela indústria Cookbem indicam que seu forno de micro-ondas tem probabilidade0,1 de apresentar a 1 a. falha antes de 900 horas de uso. Um novo método de produção está send