Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.3 - Ex. 1g

Com o auxílio da tabela t - s t u d e n t calcule:

(g) O valor de d   tal que P t 2 1 > d = 0 , 05

Passo 1

Oi mais uma vez (e última! Grazadeus).

Vamos relembrar o que definimos para resolver essa questão todinha:

P T < - t = P T > t = p

Na tabela de t-student t e uma porcentagem p c o l u n a s .

Quando temos uma probabilidade BILATERAL:

p = α

Já quando temos que encontrar uma probabilidade UNILATERAL:

p = 2 α

Passo 2

Nessa ultima alternativa, temos algo um bocado parecido com a anterior; novamente teremos que abrir o módulo.

Por acaso você se lembra dessa regrinha para módulos??

x > a → x < - a     O U     x > a

Vamos precisar disso; terremos:

P t 21 > d = P t 21 < - d     O U     x > d = 0,05

Lembra, também, da regrinha do “OU” = SOMA?

Se usarmos isso:

P t 21 < - d + P t 21 > d = 0,05

Mas nesse caso, temos de considerar os dois eventos ocorrendo independentemente; isso significa que devemos considerar duas probabilidades unilaterais:

P t 21 > d = α = p 2

E

P t 21 < - d = α = p 2

Substituindo:

P t 21 < - d ⏟ p / 2 + P t 21 > d ⏟ p / 2 = 0,05

Portanto, p = 0,05 .

Passo 3

Beleza, então só precisamos buscar na tabela de t-student a coluna que representa 5 % e a linha de 21   g r a u s   d e   l i b e r d a d e .

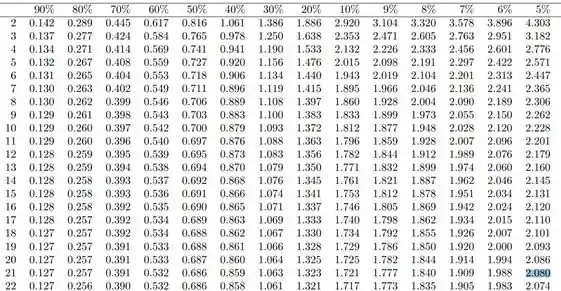
Portanto:

P t 21 < - 2,080 + P t 21 > 2,080 = 0,05

Concluindo: d = 2,080

Resposta

(g) d = 2,080

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

9-52.Semear nuvens tem sido estudado durante muitas decadas comoum procedimento de mudanca do tempo(para um estudo interessantedlesse assunto.vejao artigo em TechnomeiricsA Bavsesten Analvsisofa Malti
9-51.Uim artigo de 1992 na revista Journal ofthe American Medical Asso-ciation("A Critical Appraisal of 98,6 Degrees F.the Upper Limit of theNormal Body Temperature,and Oiher lxgacies ef Carl Reinhold
9-54.Considere os dados do coeficiente de restituicao da bola de beise-bol.apresentados no Exercicio 8-86.（a) Os dados sustentam a afirmacao de que o coeficiente medio de res-tituicao de bolas de beis
9.55.Considere a concentracao de oxigenio dissolvido em barragensno Vale do Tennessee,apresentadlos primeiramiente no Exereicio S-88.（a)Teste as hipoteses H:p=4versus H;p=4.Use a=0,01.En-contre o valo
9-57.Reconsidere o experimento de testes em pncus.descrito no Exer-cicio 8-23.（a)O engenheiro gostaria de demonstrar que a vida media desse novopneu tem um excesso de 60.000 quilometros.Formule e test