Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Meyer - Aplicações a Estatística- Ed: 2º - Capítulo 3.Problemas - Ex. 15

Cada uma de duas pessoas joga três moedas equilibradas. Qual é a probabilidade de que elas obtenham o mesmo número de caras?

Passo 1

Fala aí galera, vamos para mais uma questão de probest.

Para determinarmos a probabilidade de que duas pessoas obtenham o mesmo número de caras após jogar moedas equilibradas, temos que fazer uma árvore de probabilidades para os lançamentos. Fica assim:

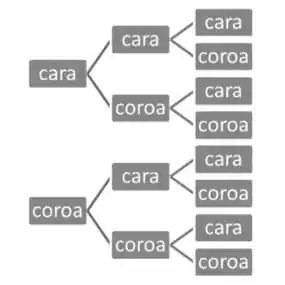
No lançamento de uma moeda equilibrada, podemos obter dois resultados: Cara ou Coroa, como demonstrado acima. Portanto, a probabilidade é 1 / 2 para ambas.

Passo 2

Em seguida, vamos enumerar os eventos possíveis:

A   →   N e n h u m a   m o e d a   m o s t r o u   c a r a B   →   U m a   m o e d a   m o s t r o u   c a r a C   →   D u a s   m o e d a s   m o s t r a m   c a r a D   →   T r ê s   m o e d a s   m o s t r a m   c a r a

E assim, calcular a probabilidade de cada um deles. Para o evento A , temos:

P A = 1 2 ∙ 1 2 ∙ 1 2 P A = 1 8

Para B , temos que apenas uma das moedas terá uma cara, ou seja, são eventos mutuamente exlucisvos, logo:

P B = 1 2 ∙ 1 2 ∙ 1 2 + 1 2 ∙ 1 2 ∙ 1 2 + 1 2 ∙ 1 2 ∙ 1 2 P B = 3 8

Já para o evento C , temos:

P C = 1 2 ∙ 1 2 ∙ 1 2 + 1 2 ∙ 1 2 ∙ 1 2 + 1 2 ∙ 1 2 ∙ 1 2 P C = 3 8

Por fim, para o último evento, temos:

P D = 1 2 ∙ 1 2 ∙ 1 2 P D = 1 8

Passo 3

Por fim, para encontrarmos a probabilidade de pedida no enunciado precisamos somar todos estes eventos, visto que eles são mutamente exclusivos. Além disso, temos esses eventos anteriores para cada pessoa, assim, seus lançamentos são eventos independentes e, por isso, devemos multiplica-los. Fica assim:

P E = 1 8 ∙ 1 8 + 3 8 ∙ 3 8 + 3 8 ∙ 3 8 + 1 8 ∙ 1 8 P E = 5 16

Resposta

P E = 5 16

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Discos de plástico de policarbonato, provenientes de um fornecedor, são analisados com relação à resistência a arranhões e a choque.Os resultados de 100 discos estão resumidos a seguir:Seja A o evento
Considere duas urnas, cada uma contendo bolas brancas e pretas. As probabilidades de se retirarem bolas brancas da primeira e da segunda urnas são, respectivamente, p e p'. Bolas são retiradas sequenc
Como um modelo simplificado de previsão do tempo, suponha que o tempo amanhã (seco ou úmido) será o mesmo de hoje com probabilidade p. Mostre que, se o tempo está seco em 1° de janeiro, então P n , a
Suponha que XeY tenham distribuição conjunta dada pela seguinte tabela.a) determine a covariância entre XeY ; b) XeY são independentes?
O Problema da Eleição. Em uma eleição, o candidato A recebe n votos e o candidato B recebe m votos, onde nm. Assumindo que todas as n + m ! n ! m ! ordens de votos sejam igualmente prováveis, suponha