Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.3 - Ex. 17
Numa caixa existem 4 bolas numeradas 3, 5, 5 e 7. Uma bola é sorteada ao acaso, seu número anotado e devolvida à caixa. Uma segunda bola é escolhida, também ao acaso, e seu número denotado por
a. Determine a conjunta de
b. Calcule as marginais de . Elas são independentes?
c. Encontre o valor esperado e a variância de .
Passo 1
Vamos resolver (a) e (b). Determinaremos a conjunta de por meio de uma tabela de dupla entrada, nessa tabela também estarão incluídas as marginais de
Note que a probabilidade de pegar uma bola numerada com 3 ou 7 na caixa é de e a probabilidade de pegar uma bola numerada com o número 5 é de , assim:
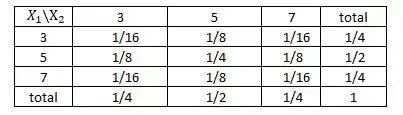
As variáveis são independentes, o primeiro evento que é a retirada da bola não interfere no segundo evento, que é a retirada da segunda bola. Isso acontece porque houve a reposição da bola retirada na primeira vez, ou seja, após acontecer o primeiro evento, na caixa ainda tem 4 bolas, assim como antes de ser retirada uma bola.
Numericamente, podemos provar da seguinte forma:
Se pegarmos qualquer ponto do corpo da tabela e multiplicar as suar marginais, teremos o valor descrito no corpo. Isso nos confirmará que as variáveis são independentes.
Passo 2
Em (c) queremos calcular a esperança e a variância de . Começando pela esperança, teremos que ela é dada por uma forma genérica da seguinte maneira:
Assim,
Para teremos:
Passo 3
A variância será dada por:
Assim,
Daí:
A variância de será dada por:
Resposta
Ei, a resposta está no passo a passo :)