Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 5.Exercícios - Ex. 23

Dois método de medir a suavedade de uma superfície são usados para avaliar um produto feito de papel. As medidas, em unidade codificadas, são registradas como desvios em relação a um valor nominal da suavidade da superfície. A distribuição de probabilidades conjuntos das duas medidas é uma distribuição uniforme na região. Ou seja para X e Y na região. Determine o valor de c estar o que seja uma função densidade de probabilidade conjunta.

Determine o seguinte:

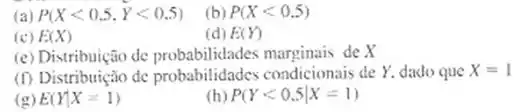
Passo 1

Temos o seguintes dados:

f ( x , y ) = c

0 < x < 4

0 < y

x - 1 < y < x + 1

Primeiro, precisamos determinar c:

∫ 0 1 ∫ 0 x + 1 f ( x , y ) d y d x + ∫ 1 4 ∫ x - 1 x + 1 f ( x , y ) d y d x =

= ∫ 0 1 ∫ 0 x + 1 c d y d x + ∫ 1 4 ∫ x - 1 x + 1 c d y d x =

= ∫ 0 1 c ( x + 1 ) d x + ∫ 1 4 2 c d x =

= 3 c 2 + 6 c =

= 15 2 c

A integral sobre todos os valores possíveis de x e y deve ser igual a 1:

15 c 2 = 1

Resolvendo para c:

c = 2 15

A função de densidade de probabilidade conjunta então se torna:

f ( x , y ) = 2 15

Passo 2

Letra a:

A probabilidade é a integral de f ao longo dos intervalos dados:

P ( X < 0.5 , Y < 0.5 ) = ∫ 0 0.5 ∫ 0 0.5 2 15 d y d x =

= ∫ 0 0.5 1 15 d x = 1 30 =

= 0.0333 . . .

Passo 3

Letra b:

A probabilidade é a integral de f ao longo dos intervalos dados:

P ( X < 0.5 ) = ∫ 0 0.5 ∫ 0 x + 1 2 15 d y d x =

= ∫ 0 0.5 2 15 ( x + 1 ) d x =

= 1 12 =

= 0.0833

Passo 4

Letra c:

O valor esperado μ é a soma do produto de cada possibilidade x com sua probabilidade P ( x ) :

E ( X ) = ∫ 0 1 ∫ 0 x + 1 2 15 x d y d x + ∫ 1 4 ∫ x - 1 x + 1 2 15 x d y d x =

= ∫ 0 1 2 15 x ( x + 1 ) d x + ∫ 1 4 4 x 15 d x =

= 1 9 + 2 =

= 19 9 =

= 2.111

Passo 5

Letra d:

O valor esperado μ é a soma do produto de cada possibilidade x com sua probabilidade P ( x ) :

E ( Y ) = ∫ 0 1 ∫ 0 x + 1 2 15 y d y d x + ∫ 1 4 ∫ x - 1 x + 1 2 15 y d y d x =

= ∫ 0 1 1 15 ( x + 1 ) 2 d x + ∫ 1 4 4 x 15 d x =

= 1 9 + 2 =

= 19 9 = 2.111 . . .

Passo 6

Letra e:

A distribuição marginal de X é f integrada sobre todos os valores possíveis de Y.

S e   0 < x < 1 :   f X ( x ) = ∫ 0 x + 1 2 15 d y =

= 2 15 ( x + 1 )

S e   1   ≤   x < 4 :   f X ( x ) = ∫ x - 1 x + 1 2 15 d y =

= 4 15

Passo 7

Letra f:

A distribuição condicional é a distribuição de probabilidade conjunta dividida pela distribuição marginal:

f Y | x = 1 ( y ) = f X Y ( 1 , y ) f X ( 1 ) = 1 2 = 0.5

Passo 8

Letra g:

O valor esperado μ é a soma do produto de cada possibilidade x com sua probabilidade P ( x ) :

E ( Y | X = 1 ) = ∫ 0 2 y f Y | x = 1 ( y ) d y =

= ∫ 0 2 1 2 y d y =

= 1

Passo 9

Letra h:

A probabilidade condicional é a integral da distribuição condicional durante o intervalo determinado:

P ( Y < 0.5 | X = 1 ) = ∫ 0 0.5 1 2 d y =

= 1 4 =

= 0.25

Resposta

  1. 0.0333
  2. 0.0833
  3. 2.1111
  4. 0.9938
  5. S e   0 < x < 1 :   f X ( x ) = ∫ 0 x + 1 2 15 d y = 2 15 ( x + 1 )

    6. S e   1   ≤   x < 4 :   f X ( x ) = ∫ x - 1 x + 1 2 15 d y = 4 15

  6. f Y | x = 1 ( y ) = 0.5
  7. 1
  8. 0.25
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Numa comunidade em que apenas dez casais trabalham, fez-se um levantamento no qual foram obtidos os seguintes valores para os rendimentos anuais:Um casal é escolhido ao acaso entre os dez. Seja X o re
Numa comunidade em que apenas dez casais trabalham, fez-se um levantamento no qual foram obtidos os seguintes valores para os rendimentos anuais:Um casal é escolhido ao acaso entre os dez. Seja X o re
A tabela abaixo dá a distribuição conjunta de X e Y. (a) Determine as distribuições marginais de X e Y. (b) Obtenha as esperanças e variâncias de X e Y. (c) Verifique se X e Y são independentes.(d) Ca
Lançam-se, simultaneamente, uma moeda e um dado. (a) Determine o espaço amostral correspondente a esse experimento. (b) Obtenha a tabela da distribuição conjunta, considerando X o número de caras no l
3. Considere a distribuição conjunta de X e Y, parcialmente conhecida, dada na tabela abaixo. (a) Complete a tabela, considerando X e Y independentes. (b) Calcule as médias e variâncias de X e Y. (c)